Indice
I numeri reali
Come abbiamo visto l'insieme $Q$ dei numeri razionali è denso; ciò significa che, ordinandoli su una retta, la differenza tra un punto e il successivo è tendente a zero. Quindi la retta $r$ su cui li rappresentiamo deve essere disegnata in modo continuo così:

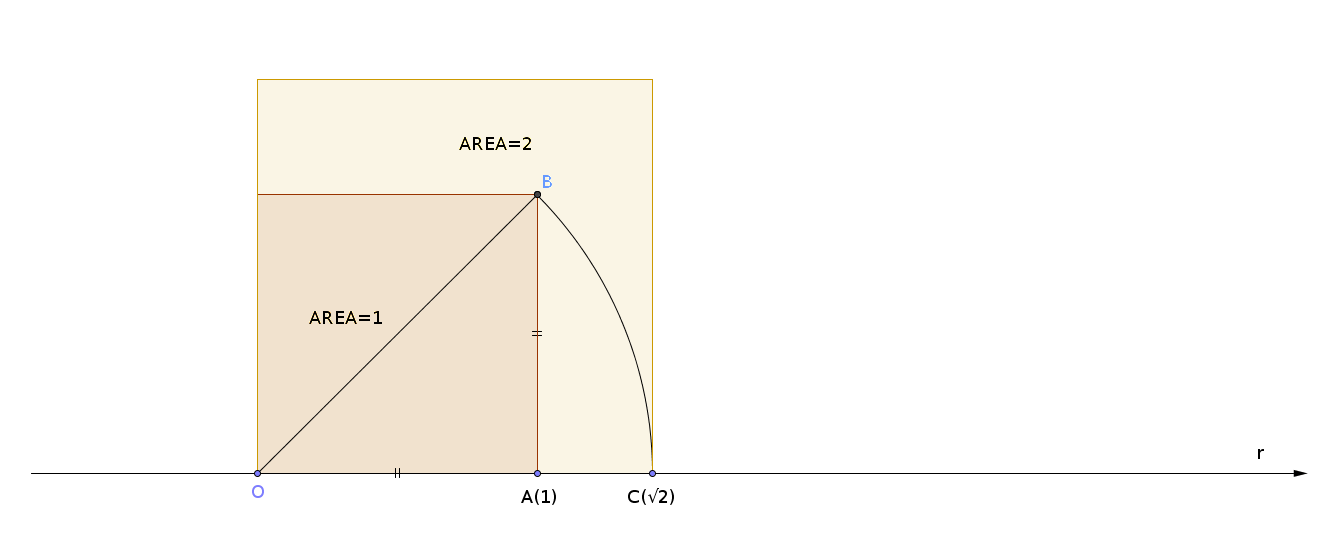
Domanda: ai punti della retta corrisponde sempre un numero razionale oppure no? In altre parole: esitono su questa retta dei numeri che non possono essere rappresentati come delle frazioni? Ci sono altri numeri oltre ai razionali? Certamente sì; osserviamo questa figura e togliamoci ogni dubbio:
Il numero $\sqrt{2}$ esiste, come esiste la diagonale del quadrato di lato 1, e come esiste il lato del quadrato di area 2.
Quindi i razionali, pur formando un insieme denso, non ricoprono tutta la retta dei numeri. Si dice che $Q$ non è completo.
Però dobbiamo ancora provare che questo nuovo numero $\sqrt{2}$ non è annoverabile tra i razionali, ossia non può essere scritto come un rapporto tra interi $\frac {p}{q}$.
Radice di 2 dimostra di essere irrazionale
E come fa a dimostrare di essere di una natura diversa da tutti i razionali? Vediamo: ragioniamo per assurdo, ovvero dimostriamo che è impossibile negare la tesi. Se ci riusciamo, saremo autorizzati ad ammetterne la validità.
Quindi supponiamo per assurdo che $\sqrt{2}$ sia razionale. Ciò significa che lo possiamo scrivere come una frazione, che immaginiamo già semplificata ai minimi termini: $\frac {p}{q}=\sqrt{2}$
Qui $p$ e $q$ sono due numeri interi. Non possono essere entrambi pari perchè abbiamo detto che la frazione è ridotta ai minimi termini (ho già semplificato un eventuale fattore 2).
Pertanto solo una delle 3 eventualità è possibile:
- sono entrambi dispari
- $p$ è dispari e $q$ è pari
- $p$ è pari e $q$ è dispari
Riscriviamo la formula $\frac {p}{q}=\sqrt{2}$ in quest'altro modo equivalente:
$p^2 =2 q^2$
Questo dimostra che il numero $p$ al quadrato è pari, visto che è multiplo di 2. Ma allora anche $p$ è pari, dato che il quadrato di un dispari è dispari e il quadrato di un pari è pari. Allora delle 3 precedenti solo l'ultima può essere vera, ovvero $p$ pari e $q$ dispari.
Ma se $p$ è pari allora può essere riscritto come il doppio di un numero $n$: $p=2n$.
Riscriviamo la formula di sopra ora che $p=2n$:
$4n^2=2q^2$
semplifichiamo:
$q^2=2n^2$
il che prova che anche $q$ è pari. Pertanto anche la 3 è falsa.
Siamo giunti alla conclusione che supporre di poter scrivere $\frac {p}{q}=\sqrt{2}$ è sbagliato, quindi $\sqrt{2}$ è irrazionale.
...e ce ne sono anche infiniti altri
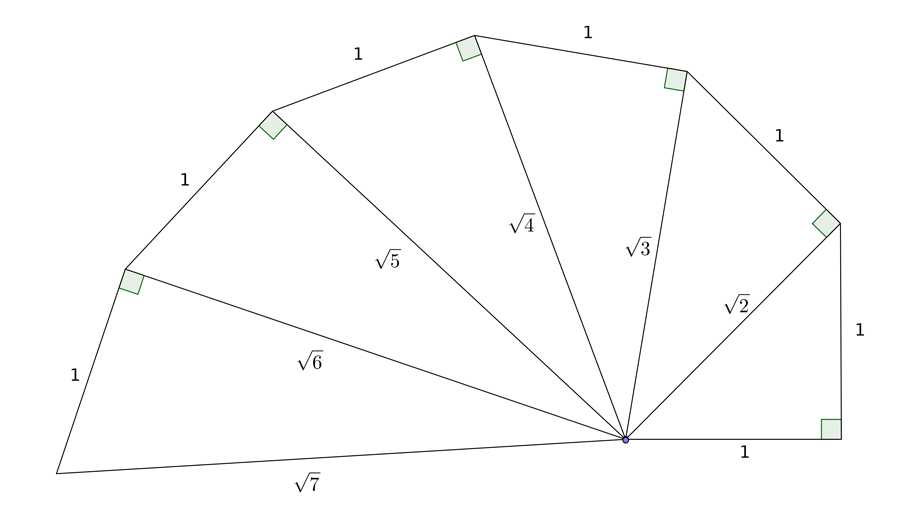
A partire dal numero $\sqrt{2}$ si possono costruire altri numeri irrazionali, come mostra questa figura:
Con una dimostrazione del tutto analoga alla precedente si può dimostrare che anche $\sqrt{3}, \sqrt{5}$ ecc. sono irrazionali. Prova tu a dimostrare l'irrazionalità di $\sqrt{3}$!
Si può dimostrare, ma con una matematica superiore, per esempio che i nonstri numeri preferiti $\pi$ e $e$ sono irrazionali. Ecco una bellissima dimostrazione dell'irrazionalità di $\pi$:
I numeri reali
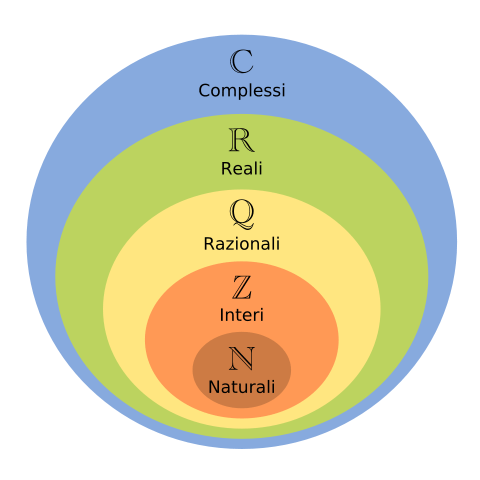
L'unione dei numeri razionali e dei numeri irrazionali forma l'insieme dei numeri reali, che indicheremo con il simbolo $R$ o $\mathbb{R}$
I reali contengono al loro interno i razionali:
Vedremo i numeri complessi in seguito. Per ora basta anticipare che anche nell'insieme $R$ c'è un'operazione che non ha significato, ovvero la radice con indice pari dei numeri negativi. L'insieme dei numeri complessi darà un significato anche a operazioni quali $\sqrt{-1}$.
Proprietà dell'insieme $R$
Riassumendo, l'insieme dei numeri reali gode delle seguenti proprietà (ce ne sono anche altre a dire la verità, ma noi ci fermiamo qui):
Definizione di numero reale
Ogni numero reale può essere definito come l'elemento separatore tra due classi contigue di numeri razionali.