Indice
La vera natura del magnetismo
Rifletteteci bene: qual è la vera origine della forza del campo magnetico? Nel caso stazionario, per l'ipotesi di Ampere l'origine del campo magnetico è sempre una corrente, sia essa elettrica oppure atomica.
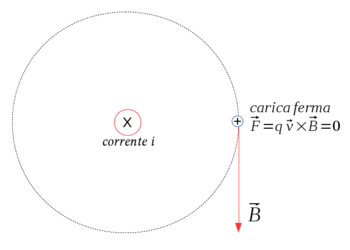
Giusto. Ma perché una carica in moto sperimenta una forza quando si trova nel campo magnetico generato da una corrente? Abbiamo una forza di Lorentz, direte voi. Perfetto, dico io. Da quale sistema di riferimento state esaminando il fenomeno? Da quello del laboratorio in cui la carica viene vista muoversi, vero? Mettetevi ora nel riferimento della carica elettrica. La state seguendo e in questo riferimento essa appare ferma. Quanto vale qui la forza di Lorentz? È nulla!
- Huston, abbiamo un problema!
- Qual è il problema, comandante?
- Il principio di relatività è il nostro problema! Lui richiede che la fisica nei due riferimenti sia la stessa, ma nel riferimento dove la carica è ferma non c'è alcuna forza!
- E allora?
- E allora che dobbiamo fare? Abbandoniamo il principio di relatività o riscriviamo la fisica?
- La seconda che hai detto…
La soluzione di Einstein
Ecco qual era il grattacapo (più o meno) su cui stava lavorando Albert Einstein agli inizi del Novecento, ecco lo studio da cui prese le mosse la teoria della relatività. Le leggi dell' elettromagnetismo sembravano non obbedire al principio di relatività. La sua soluzione fu semplicissima: il campo magnetico può essere reinterpretato come una correzione relativistica della legge di Coulomb; in altre parole, è sufficiente la legge di Coulomb per fare tutto l' elettromagnetismo. Non è meraviglioso 
La logica che c'è sotto, se teniamo conto degli effetti relativistici, è anche facilmente comprensibile: nel riferimento della carica è il filo a muoversi, e per la relatività delle lunghezze le cariche del filo aumentano la loro densità. Gli elettroni di conduzione, però, vengono visti andar ancor più veloci delle cariche positive, in quanto si muovono anche per via della conduzione. Pertanto vi è una disparità tra la forza elettrostatica dovuta ai protoni e quella dovuta agli elettroni. Il risultato è una forza elettrostatica netta che, a conti fatti, equivale proprio a quella che si calcola con le leggi del magnetismo.
La cosa che può sembrare strana è come possano esserci effetti macroscopici a causa di velocità così basse ($\approx 10^{-5}m/s$) come quelle con cui derivano gli elettroni di conduzione. Si tratta però di una quantità sterminata di elettroni…
Vediamo i dettagli.
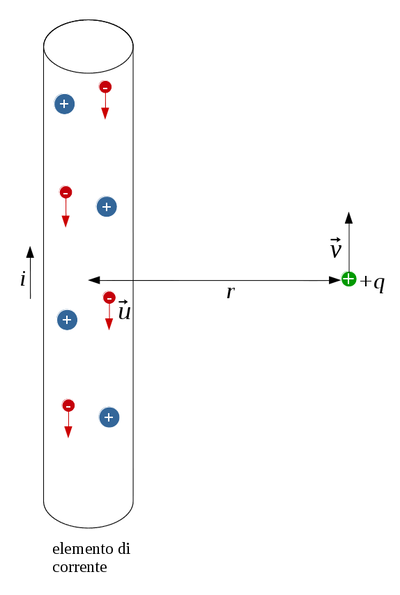
Nel riferimento del laboratorio
Ecco il filo percorso da corrente $i$ nel riferimento del laboratorio. La carica $q$, per convenzione positiva, si muove a velocità $\vec v$, mentre gli elettroni di conduzione hanno una velocità ordinata $\vec u$. La corrente nel filo è dovuta agli elettroni negativi, ma come sappiamo va rappresentata con verso contrario al loro movimento. La deriva degli elettroni è molto piccola, specialmente se confrontata con la velocità della luce $c$, ed in genere è dell'ordine dei $10^{-5}m/s$.
In questo sistema di riferimento la forza del campo magnetico viene interpretata in termini di forza di Lorentz: $\vec F = q \vec v \times \vec B$. Il modulo della forza vale semplicemente $qvB$ se la velocità è parallela al filo.
Ma per la legge di Biot-Savart il campo magnetico del filo, a distanza $r$ da esso, si calcola così:
$$ B = \frac{\mu_0}{2\pi}\frac{i}{r} $$
Pertanto il modulo della forza magnetica si può scrivere:
\begin{equation} \label{b-s} F = \frac{\mu_0}{2\pi}\frac{qvi}{r} \end{equation}
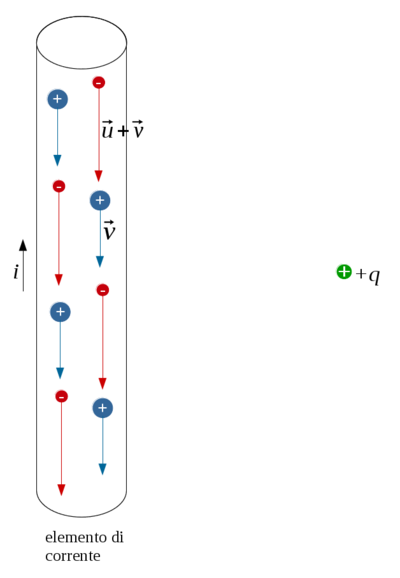
Nel riferimento della carica in moto
Vediamo che lo stesso risultato possiamo ottenerlo anche nel riferimento che segue la carica $q$, in cui la carica è ferma. Da un punto di vista classico non si spiega per quale motivo essa debba essere attratta dal filo, visto che la forza di Lorentz è nulla.
Il filo non esercita neanche una azione elettrostatica su di essa, perchè il filo non è elettricamente carico, e la densità lineare di carica delle cariche negative $\lambda^-$ è uguale a quella delle cariche positive $\lambda^+$. Pertanto la densità di carica totale è nulla.
Tutto il filo si muove verso il basso a velocità $\vec v$, quindi anche i nuclei atomici positivi vengono visti spostarsi a questa velocità. Gli elettroni di conduzione pure, ma ad essa vanno a sommare anche la velocità di deriva $\vec u$. Quindi le cariche negative si muovono più velocemente.
Il risultato è che dal punto di vista della carica $q$, per la relatività delle lunghezze, la distanza tra le cariche positive si riduce. Ma le cariche negative sono più veloci delle positive, quindi l'effetto dell'aumento della densità lineare di carica è più marcato per le cariche negative.
E se aumenta la densità lineare di carica aumenta il campo elettrico e quindi la forza.
Il calcolo della densità lineare di carica del filo
Da qui in poi, per brevità, useremo il termine abbreviato “densità di carica” per intendere la “densità lineare di carica”.
Il campo elettrico $E$ generato da un filo avente densità di carica $\lambda$, a distanza $r$ da esso si calcola così:
\begin{equation} \label{E} E = \frac{1}{2\pi\epsilon_0}\frac{\lambda}{r} \end{equation}
ed è diretto radialmente con verso uscente o entrante a seconda che la densità di carica sia positiva o negativa rispettivamente.
È chiaro che un conduttore genera un campo elettrico solo se ha delle cariche in eccesso, ovvero quando ha una densità di carica diversa da zero. Questo a prescindere dal fatto che sia attraversato da corrente o meno.
Qui però, per quanto detto sopra, la sua densità di carica NON è più nulla, in quanto le cariche negative si contraggono di più di quelle positive (raggiungono una densità maggiore). Conviene riscrivere la densità di carica del filo come:
$$ \lambda = \lambda^+ + \lambda^- $$
dove $\lambda^+$ e $\lambda^-$ sono le densità delle cariche positive e negative rispettivamente. Per definizione la densità di carica è la quantità di carica per unità di lunghezza:
$$ \lambda^+ = \frac{+q}{L_0} = +\lambda_0 \\ \lambda^- = \frac{-q}{L_0} = -\lambda_0 $$
Ma la lunghezza si contrae relativisticamente, quindi dobbiamo sostituire $L_0$ con $L$ che è la lunghezza effettivamente misurata:
$$ L = L_0 \sqrt{1-\frac{v^2}{c^2}} $$
dove $L_0$ è la lunghezza propria, misurata a riposo.
Ora teniamo conto dela fatto che le cariche positive si muovono a velocità $v$, mentre quelle negative si muovono a velocità $u+v$. Quindi tenendo conto della relativita_delle_lunghezze le densità di carica precedenti diventano:
\begin{equation} \lambda^+ = \frac{+q}{L} = \frac{+q}{L_0 \sqrt{1-\dfrac{v^2}{c^2}}} = +\lambda_0 \left(1-\frac{v^2}{c^2}\right)^{-1/2} \label{l+} \end{equation}
\begin{equation} \lambda^- = \frac{-q}{L} = \frac{-q}{L_0 \sqrt{1-\dfrac{(v+u)^2}{c^2}}} = - \lambda_0 \left(1-\dfrac{(v+u)^2}{c^2}\right)^{-1/2} \label{l-} \end{equation}
dove abbiamo indicato con $\lambda_0$ la densità di carica a riposo.
Ora, poichè il fattore $v/c$ è infinitesimo, possiamo usare la seguente regola di approssimazione, che vale se $a \thickapprox 0$:
$$ (1+a)^n \thickapprox 1+na $$
Allora le densità di carica $\eqref{l+}$ e $\eqref{l-}$ diventano rispettivamente:
\begin{equation} \lambda^+ = +\lambda_0 \left (1-\frac{v^2}{c^2}\right)^{-1/2} \thickapprox +\lambda_0 \left(1+\frac{v^2}{2c^2}\right) \label{l3} \end{equation}
\begin{equation} \lambda^- = - \lambda_0 \left(1-\frac{(v+u)^2}{c^2}\right)^{-1/2} \thickapprox - \lambda_0 \left(1+\frac{(v+u)^2}{2c^2}\right) \label{l4} \end{equation}
$\lambda^-$ può essere ulteriormente semplificato visto che la velocità $u$ degli elettroni di conduzione è dell'ordine di $10^{-5}m/s$, quindi in genere molto minore di $v$:
\begin{equation} \lambda^- = - \lambda_0 \left(1+\frac{(v+u)^2}{2c^2}\right) = - \lambda_0 \left(1+\frac{v^2+2vu+u^2}{2c^2}\right) \thickapprox - \lambda_0 \left(1+\frac{v^2+2vu}{2c^2}\right) \label{l5} \end{equation}
dove abbiamo trascurato $u^2$, che è molto piccolo in confronto agli altri termini della somma (infinitesimo di ordine superiore).
Finalmente siamo in grado di scrivere la densità di carica totale sommando la $\eqref{l3}$ e la $\eqref{l5}$:
\begin{equation} \label{l_final} \lambda = \lambda^+ + \lambda^- = +\lambda_0 \left(1+\frac{v^2}{2c^2}\right) - \lambda_0 \left(1+\frac{v^2+2vu}{2c^2}\right) = - \lambda_0 \frac{\not 2vu}{\not 2c^2} = - \lambda_0 \frac{vu}{c^2} \end{equation}
E finalmente la forza magnetica
E abbiamo finito (quasi)! Per la $\eqref{E}$ e la $\eqref{l_final}$ il campo elettrico $E$ e dunque la forza $F=qE$ sono:
\begin{equation} \label{F} F = qE = q \frac{\lambda}{2\pi\epsilon_0 r} = -q \frac{\lambda_0}{2\pi\epsilon_0 r} \frac{vu}{c^2} \end{equation}
Il segno $-$ indica che la forza elettrostatica che abbiamo calcolato è attrattiva, come ci aspettiamo in quanto lo è anche la forza di Lorentz.
Rimane da dimostrare che tutto ciò è uguale all'espressione della forza ricavata nel riferimento del laboratorio:
$$ F = \frac{\mu_0}{2\pi}\frac{qvi}{r} $$
Facciamo entrare in gioco la corrente che circola nel filo, che per definizione è la quantità di carica $Q$ che attraversa la sezione del filo nel tempo $t$:
\begin{equation} \label{i} i = \frac {Q}{t} = \frac{L_0}{t}\cdot\frac{Q}{L_0} = u \cdot \lambda_0 \end{equation}
questo perchè se la lunghezza $L_0$ viene attraversata dalla carica $Q$ nel tempo $t$ la velocità degli elettroni sarà $u=L_0/t$. Invece $Q/L_0$ altro non è che la solita densità di carica $\lambda_0$.
Mettiamo a sistema la corrente $\eqref{i}$ con l'espressione della forza $\eqref{F}$, ricordando quel che ci ha lasciato Maxwell riguardo al modo in cui calcola la velocità della luce $c$:
$$ c = \frac{1}{\sqrt{\epsilon_0\mu_0}} \qquad \implies \qquad c^2 = \dfrac{1}{\epsilon_0\mu_0} $$
Forza con il sistemino allora:
$$ \begin{cases} c^2 = \dfrac{1}{\epsilon_0\mu_0} \\ i = u \lambda_0 \\ F = -q \dfrac{\lambda_0}{2\pi\epsilon_0 r} \dfrac{vu}{c^2} \end{cases} $$
e così si dimostra facilmente che 
$$ F = -\frac{\mu_0}{2\pi}\frac{qvi}{r} = -qv\left ( \frac{\mu_0}{2\pi}\frac{i}{r} \right )$$
che è la forza di Lorentz $\eqref{b-s}$, ricavata però facendo a meno del campo magnetico, che divenda una correzione relativistica della legge di Coulomb.