Le quattro equazioni di Maxwell riassumono le proprietà generali dell'elettricità e del magnetismo. Esse ci dicono che cosa si deve fare per generare un campo elettrico e un campo magnetico.

Con una teoria basata su queste quattro equazioni, nel 1864 James Clerck Maxwell, riuscì a prevedere l'esistenza delle onde elettromagnetiche.

L'esperimento di Hertz (1887), nel rivelare l'effettiva esistenza delle onde elettromagnetiche, sancì il trionfo della teoria di Maxwell e dell'intero elettromagnetismo, le cui leggi non erano certo state elaborate per dare risposte alla questione secolare dell'essenza della luce, tanto meno per prevedere l'esistenza di radiazioni fino ad allora sconosciute.

Ma nonostante i fisici del tempo si illusero che fosse stata messa la parola fine sul problema della luce, ai primi del '900 la questione si riaprì con la teoria quantistica del fotone.

Il fatto che la teoria dell'elettromagnetismo abbia previsto fenomeni nuovi, andando ben oltre la semplice spiegazione dei fatti sperimentali dai quali essa aveva preso le mosse, può essere considerato una prova molto potente della bontà di questa teoria.

L'impatto di questa teoria scientifica nella qualità nella vita degli uomini fu notevole: nel 1901 l'italiano Guglielmo Marconi avviò l'era delle comunicazioni radio (senza fili) inviando segnali dal Canada all'Inghilterra, risultato che gli valse il premio Nobel.

Le equazioni di Maxwell sono il raggruppamento del teorema di Gauss e della circuitazione di $\vec E$ e $\vec B$. E' inutile dire che è necessario conoscere qui il concetto di flusso di un vettore e di circuitazione di un vettore. Se non ricordi questi due concetti fermati un attimo (momento, momento!! non ho detto di alzarti dalla sedia!!) e recupera questi argomenti dal libro.

$ \phi (\overrightarrow{E})=\displaystyle{\int_{\Omega}} \overrightarrow{E} \cdot \overrightarrow{dS}=\dfrac{\sum Q}{\epsilon} $

$ \phi (\overrightarrow{B})=\displaystyle{\int_{\Omega}} \overrightarrow{B} \cdot \overrightarrow{dS}=0 $

$ \Gamma (\overrightarrow{E}) = \displaystyle{\oint} \overrightarrow{E} \cdot \overrightarrow{dl}=-\dfrac{d{\phi (\overrightarrow{B})}}{dt} $

$ \Gamma (\overrightarrow{B}) = \displaystyle{\oint} \overrightarrow{B} \cdot \overrightarrow{dl}=\mu \left(\sum i +\epsilon \dfrac{d{\phi (\overrightarrow{E})}}{dt}\right) $

Diamo ora una lettura delle quattro equazioni prendendole in esame singolarmente. Alla fine cercheremo di darne una visione d'insieme e sarà fatta… luce (vi è piaciuta, eh? non l'avete capita? allora rileggete il cappello.. il cappello.. si, quello in alto .

Per vostra comodità, riporterò ciascuna equazione scrivendone la formula, leggendone il significato matematico, dandone una interpretazione sintetica e infine una interpretazione più approfondita.

$ \phi (\overrightarrow{E})=\displaystyle{\int_{\Omega}} \overrightarrow{E} \cdot \overrightarrow{dS}=\dfrac{\sum Q}{\epsilon} $

Il flusso del campo elettrico attraverso una qualunque superficie chiusa è uguale alla quantità di carica in essa contenuta (non contano le cariche esterne) fratto la costante dielettrica.

Un campo elettrostatico può essere generato da cariche libere, isolate.

Qualcuno si potrebbe chiedere dove sia finita la legge di Coulomb, e perchè non si è riservato a lei il ruolo di legge fondamentale dell'elettrostatica. Ma il teorema di Gauss non è conseguenza della legge dell'inverso del quadrato? La stessa legge implicava che le cariche in eccesso in un conduttore carico si disponessero nella sua superficie, e che lo stesso conduttore rappresentasse uno schermo elettrostatico. Oltre a ciò val la pena ricordare la facilità di calcolo che si guadagna quando si fa uso del teorema di Gauss, e che dal teorema di Gauss deriva il teorema di Coulomb.

Dentro quella superficie di Gauss dovete veder racchiusi tuoni e fulmini, atomi e molecole, sapori e profumi, l'intera chimica, la gabbia di Faraday, i motori elettrostatici.

$ \phi (\overrightarrow{B})=\displaystyle{\int_{\Omega}} \overrightarrow{B} \cdot \overrightarrow{dS}=0 $

Il flusso del campo magnetico attraverso una qualunque superficie chiusa è uguale a zero.

Come sarebbe embè? Non lo vedete che vi sta dicendo che Nord e Sud non possono stare separati, che mai e poi mai riuscireste a mettere uno dei due dentro un qualunque palloncino di Gauss? Questa è una delle differenze sostanziali tra elettricità e magnetismo. Dunque:

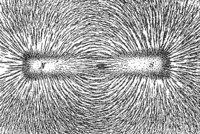
Non esiste il monopolo magnetico. Un campo magnetico è generato da dipoli magnetici.

Dovete vedere in questa legge tutti i fenomeni magnetici fondamentali. Ad esempio l'impossibilità di separare i poli spezzando in tante parti una calamita.

Le linee del campo magnetico indotto sono concatenate con quelle del campo magnetico. Cambiando il verso della corrente nell'elettromagnete cambia anche l'orientazione del campo elettrico indotto.

$ \Gamma (\overrightarrow{E}) = \displaystyle{\oint} \overrightarrow{E} \cdot \overrightarrow{dl}=-\dfrac{d{\phi (\overrightarrow{B})}}{dt} $

La circuitazione del campo elettrostatico è uguale alla derivata del flusso del campo magnetico rispetto al tempo cambiata di segno.

Ho capito. Volete l'ovetto Kinder per arrivare alla fine? Va bene, va bene… ve lo do dopo l'ovetto Kinder, ma prima cercate di afferrare bene la portata di questa equazione: il campo elettrico e quindi la corrente che alimenta il monitor sul quale punti gli occhi viene generato da campi magnetici variabili. Le linee di questo campo elettrico non sono aperte come quelle del vecchio campo elettrostatico, ma si attorcigliano chiudendosi attorno a quelle del campo magnetico (si dice che sono concatenate).

Quindi in generale il campo elettrico NON è conservativo. Ma se questo campo viene generato nel modo già evidenziato dalla prima equazione (campo elettrostatico delle cariche libere) allora questo campo è conservativo e le sue linee sono aperte e non si chiudono mai su se stesse. Non fanno vortici insomma.

In breve: un campo elettrico può essere generato da campi magnetici variabili, oltre che da cariche libere.

E che volete di più?

In base all'ipotesi di Maxwell tra le due armature del consdensatore ha origine un campo magnetico variabile nel tempo, nella stessa regione di spazio.

$ \Gamma (\overrightarrow{B}) = \displaystyle{\oint} \overrightarrow{B} \cdot \overrightarrow{dl}=\mu \left(\sum i + \epsilon \dfrac{d{\phi (\overrightarrow{E})}}{dt}\right) $

La circuitazione del campo magnetico è uguale alla somma di un termine che rappresenta la legge della circuitazione di Ampere e da un altro, che rappresenta la corrente di spostamento, che è uguale alla costante dielettrica moltiplicata per la derivata del flusso del campo elettrico rispetto al tempo.

Allora ve la metto un po' a fuoco, però cercate di stare un po' attenti.

Analizziamo un termine alla volta:

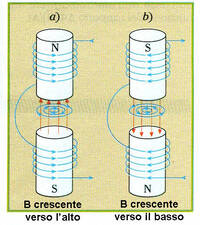
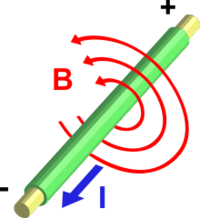
• il primo $\mu \sum i$ dice che un campo magnetico può essere generato da correnti stazionarie (costanti nel tempo). Questo campo magnetico non è conservativo, quindi le sue linee sono concatenate con la corrente $i$ che l'ha generato.
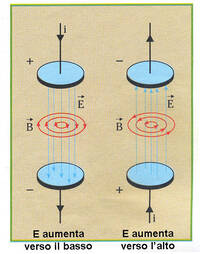
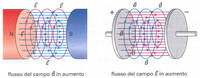
• il secondo è la famosa corrente di spostamento. Dice che un campo magnetico può essere generato anche da un campo elettrico variabile. Anche questo campo non è conservativo e le sue linee sono concatenate con quelle del campo elettrico che l'ha generato, come si vede dalla figura a fianco.

Riassumendo: un campo magnetico può essere generato da una corrente stazionaria o da un campo elettrico variabile. Le sue linee sono sempre chiuse, infatti $B$ non è mai conservativo.

Domanda: perchè la conservatività assicura che linee siano aperte e viceversa? Non ho chiesto se lo sai o no. Ho chiesto di cercare la risposta, che tanto lo so che la risposta è no. Va bè, va bè ad eccezion fatta per te, si..

La risposta è nella pagina della circuitazione di un vettore.

• Il teorema di Ampere ci dice qual è la natura stessa del magnetismo: le correnti atomiche chiuse sono responsabili del campo dei magneti permanenti. Una corrente chiusa e un elettromagnete possono essere considerati equivalenti a un dipolo magnetico. Questo spiega l'interazione magnete-corrente ed anche l'interazione corrente-corrente. Anche una singola carica libera equivale a una corrente e questo implica che la forza di Lorentz sia contemplata in questa legge. Vedeteci qui dentro il motore elettrico, la dinamo, il tubo a raggi catodici, lo spettrometro di massa.

• L'aggiunta della cosiddetta “corrente di spostamento” è una genialata di Maxwell, il quale non gradiva la mancanza di simmetria tra le ultime due equazioni: se un campo magnetico variabile genera un campo elettrico, perchè non deve succedere il contrario? (La fisica è ricca di fenomeni simmetrici, sai fare un altro esempio? che? L'ovetto Kinder?). Riuscì a determinare questo termine mancante nel tentativo di risolvere il famoso “paradosso di Ampere”. Con l'aggiunta di questo termine si può immaginare la genesi di una perturbazione elettromagnetica: è sufficiente far oscillare la tensione in un circuito perchè si generi un campo magnetico variabile, che per la terza legge genera un campo elettrico variabile con la stessa frequenza e così via.

Il moto delle cariche in una antenna (a sinistra) può essere assimilato a quello di un semplice dipolo oscillante (a destra).

$\phi (\overrightarrow{E}) = \displaystyle{\int_{\Omega}} \overrightarrow{E} \cdot \overrightarrow{dS}=0$ (non ci sono cariche)

$\phi (\overrightarrow{B}) = \displaystyle{\int_{\Omega}} \overrightarrow{B} \cdot \overrightarrow{dS} = 0$

$\Gamma (\overrightarrow{E}) = \displaystyle{\oint} \overrightarrow{E} \cdot \overrightarrow{dl}=-\dfrac{d{\phi (\overrightarrow{B})}}{dt}$

$\Gamma (\overrightarrow{B}) = \displaystyle{\oint} \overrightarrow{B} \cdot \overrightarrow{dl}=\mu\epsilon\dfrac{d{\phi (\overrightarrow{E})}}{dt}$ (non ci sono correnti)

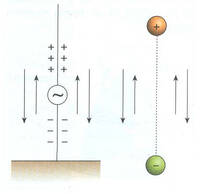
Immaginiamo di far variare il campo alettrico facendo oscillare periodicamente le cariche elettriche in un lungo cavo elettrico collegato ad un alternatore (chiamiamola pure antenna trasmittente, fig. a fianco).

La quarta equazione ci dice che questo campo elettrico variabile genera un campo magnetico a sua volta variabile. Le linee di questo campo magnetico sono concatenate con quelle del campo elettrico (vedi figura).

Per la terza equazione (eq. di Faraday-Newmann), questo campo magnetico indotto genera a sua volta un campo elettrico con esso concatenato, che a sua volta, essendo anch'esso variabile, induce ancora un campo magnetico e così via.

Un campo magnetico variabile genera un campo elettrico (a sinistra) così come un campo elettrico variabile genera un campo magnetico (a destra).

Dall'antenna viene quindi emessa una radiazione elettromagnetica che ha una frequenza uguale a quella dell'impulso iniziale. Essa si propaga alla velocità della luce, che venne ricavata dalla teoria stessa:

$ c = \dfrac{1}{\sqrt{\large{\epsilon \mu}}}=300.000 Km/s$

E il fatto che la teoria prevedesse una velocità esattamente uguale alla velocità della luce già allora conosciuta fu una prova della bontà della teoria.

Come si vede non c'è traccia in queste equazioni di un mezzo materiale dove si debbano propagare necessariamente queste onde elettromagnetiche. Infatti, a differenza del suono, che consiste nella vibrazione di un mezzo materiale elastico, la luce è vibrazione del campo elettrico e del campo magnetico insieme.