Densità lineare di carica
In filo conduttore carico, la densità lineare di carica $\lambda$ è la quantità di carica in eccesso contenuta nell'unità di lunghezza:
$$ \lambda = \frac{Q}{L} $$
Si misura quindi in $C/m$.
In parole povere ci dice quanta carica in eccesso vi è in ogni metro di filo. Notare che un filo attraversato di corrente ha una densità di carica nulla, perchè la densità delle cariche positive è uguale e contraria a quella delle cariche negative che, pur muovendosi, non aumentano per questo la loro densità.
Il campo elettrico a distanza $r$
Se vi è equilibrio elettrostatico il campo elettrico $\vec E$ deve essere perpendicolare al filo, pena ammettere una corrente superficiale di carica, ma abbiamo detto che le cariche sono in equilibrio. Inoltre, per motivi di simmetria, il campo deve avere un valore costante ad una certa distanza $r$ dal filo.
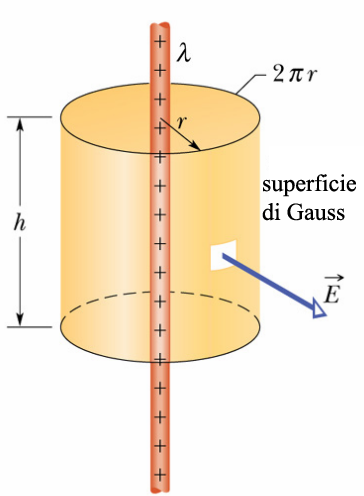
Scegliamo pertanto una superficie di Gauss che ci faciliti al massimo i calcoli, ovvero abbia il vettore superficie parallelo al campo $\vec E$ e i cui punti siano equidistanti dal filo. E cosa può essere questa superficie? Un cilindro come quello in figura.
Calcoliamo il flusso di $\vec E$ prima con il teorema di Gauss e poi con la definizione stessa di flusso.
Con il teorema di Gauss
$$ \Phi(\vec E) = \frac{Q}{\epsilon_0} $$
dove $Q$ è la carica interna alla superficie.
In base alla definizione di flusso
Il flusso totale è dato dalla somma dei flussi attraverso la superficie laterale, inferiore e superiore. Gli ultimi due sono però nulli in quanto la superficie è perpendicolare ad $\vec E$ rendendo nullo il prodotto scalare.
Rimane dunque il flusso attraverso la superficie laterale $\vec S$:
$$ \Phi(\vec E) = \vec E \circ \vec S = E~S~\cos 0 = E~S $$
La superficie laterale del cilindro è $S = 2\pi r ~h$, quindi:
$$ \Phi(\vec E) = E ~ 2\pi r ~h $$
Ora confrontiamo
Confrontando i due risultati trovati abbiamo:
$$ E ~ 2\pi r ~h = \frac{Q}{\epsilon_0} $$
E ricordando che la densità lineare di carica é $\lambda = Q/h$, il modulo di $\vec E$ diventa:
$$ E = \dfrac{1}{2\pi\epsilon_0}\frac{\lambda}{r} $$