Le maree

Le forze di marea sono dovute a un residuo differenziale della forza di gravità che agisce su un corpo che si trova in “volo libero” nel campo gravitazionale di un altro corpo. Come sappiamo un esempio di volo libero è il moto di un satellite.

In questa pagina, tanto per fissare le idee, considereremo il sistema Sole-Terra.

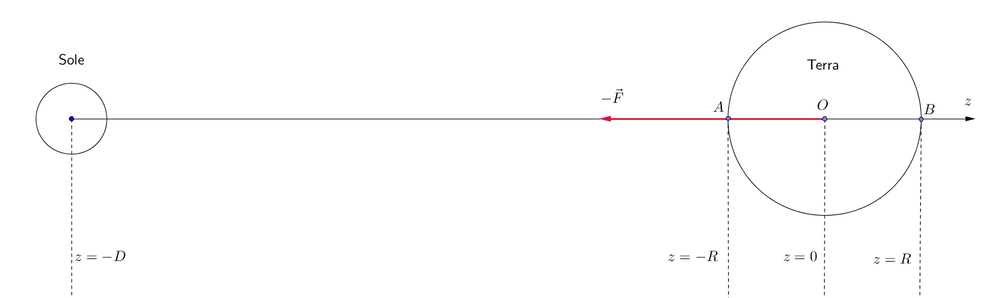
Che significa “residuo differenziale” sarà chiaro solo alla fine di questa pagina. In breve, significa che l'effetto delle maree NON è dovuto alla forza di gravità come la si percepisce solitamente, visto che è assente nel suo complesso nel riferimento terrestre, ma al fatto che essa è diversa nei vari punti della Terra, poichè -a rigore- i punti della superficie terrestre hanno diversa distanza dal Sole. Ad esempio, nella figura seguente, il punto $A$ sperimenta una forza di gravità maggiore che in $B$.

Nella figura la forza di gravità ha segno negativo perchè orientata con verso contrario all'asse $z$. Questa forza, nel centro della Terra (punto $O$), ha valore:

$$ F = -G\frac{M_{Sole}M_{Terra}}{D^2} $$

dove $D$ è la distanza Terra-Sole.

Anzichè considerare la forza di gravità consideriamo il campo gravitazionale del Sole nel centro della Terra:

$$ g = -\frac{F}{M_{Terra}} = -G \frac{M_{Sole}}{D^2}$$

Da qui in poi indicheremo più semplicemente con $M$ la massa del Sole, o in generale la massa del corpo che genera il campo.

Nei punti dell'asse $z$ il campo gravitazionale del Sole varia con questa espressione:

$$ g(z) = - G \frac{M}{{(D+z)}^2}$$

Nella superficie della Terra (punti $A$ e $B$) $z$ è piccolo in confronto a $D$ ($z \ll D $), cioè il rapporto $z/D$ è infinitesimo.

Se $z$ è infinitesimo, come lo è ad esempio all'interno del cerchio, possiamo sostituire la curva $g(z)$ con la retta tangente.

Facciamo quindi un'approssimazione nel calcolo di $g(z)$ prendendo la tangente al posto della curva; come si vede dal grafico non c'è una differenza apprezzabile se $z$ è piccolo.

L'equazione della tangente alla curva nel punto $P(0,g(0))$ è:

$$ g(z) = g(0) + g'(0)\cdot z$$

Quando $z=0$ abbiamo

$$g(z=0) = -G \frac{M}{D^2}$$

La derivata generica di $g(z)$ è

$$ g'(z) = 2G\frac{M}{(D+z)^3} $$

quindi la derivata calcolata in $z=0$ vale

$$ g'(0)=2G\frac{M}{D^3} $$

Pertanto l'espressione approssimata del campo gravitazionale sull'asse $z$ diventa

$$ g(z) = -G \frac{M}{D^2} + 2G\frac{M}{D^3}z \qquad \qquad \text{per} \quad z \ll D $$

Il primo termine è il più importante, molto più grande del secondo (sai dire perchè?). È il campo che agisce sulla Terra nel suo complesso. Il secondo è un termine differenziale, che dipende da $z$, dunque diverso per ciascun punto dell'asse $z$.

La cosa importante è che la Terra è in “volo libero” nel campo del Sole. Questo vuol dire che nel sistema di riferimento della Terra non si avverte il peso dovuto alla forza di gravità del Sole. Perciò nel riferimento terrestre possiamo trascurare il termine $-G\frac{M}{D^2}$, perchè è compensato dalla accelerazione centrifuga.

Dunque nel sistema di riferimento terrestre rimane solo il termine più piccolo (il residuo differenziale di cui parlavamo), e possiamo scrivere

\begin{equation} \label{gm} g(z) = 2G \frac {M}{D^3}z \end{equation}

Nei punti $A$ e $B$ abbiamo

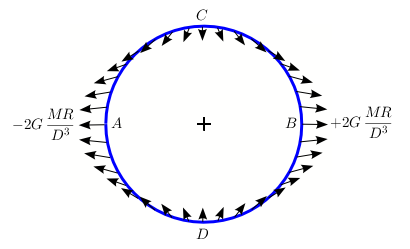
$$ \text{punto } A \qquad z=-R \qquad g(-R)=-2G\frac{MR}{D^3}\\ \text{punto } B \qquad z=+R \qquad g(+R)=+2G\frac{MR}{D^3} $$

dove $R$ è il raggio della Terra.

Quindi il campo cambia di segno e tende a far diminuire il peso, non solo nei punti della superficie più vicini al Sole, ma anche in quelli diametralmente opposti. Ecco perchè le maree si verificano approssimativamente due volte al giorno.

Nei punti $C$ e $D$ il campo è identico perchè hanno la stessa distanza dal Sole e si può dimostrare che è diretto verso il centro della Terra come mostrato in figura. Qui le masse anzichè pesare di meno pesano di più e le acque si abbassano.

Abbiamo fatto il calcolo con il Sole perchè è naturale accettare che la Terra sia in caduta libera rispetto al Sole. Se avessi iniziato la discussione dicendo che la Terra cade sulla Luna molti avrebbero preso a ridere, n'èvvero ? Eppure le maree lunari si calcolano allo stesso modo, basta sostituire $M$ con la massa della Luna e $D$ con la distanza Terra-Luna; si scopre che il fattore $M/D^3$ della Luna è più del doppio di quello del Sole. Questo per via del fatto che la dipendenza dalla distanza è molto più importante rispetto a quella sulla massa in quanto essa compare alla terza potenza.

Le maree più intense si hanno -in linea di principio- quando gli effetti di Luna e Sole si cumulano, quindi nei periodi di Luna piena e di Luna nuova. Ma ci sono anche fattori geografici che determinano le altezze delle maree; per esempio nel Mediterraneo essi sono minori che nelle coste oceaniche. In certe baie a forma di cumulo le correnti di marea scatenano sollevamenti anche di 20 metri! Le maree più marcate si hanno nella baia di Fundy nella Nuova Scozia in Canada; qui l'oscillazione delle acque tra alta e bassa marea ha delle frequenze molto vicine alla frequenza propria di oscillazione del sistema della baia, favorendo una risonanza che amplifica l'energia di oscillazione. È un po' quello che ci capita di vedere ad esempio quando, stesi nel bagnasciuga di una spiaggia, un'onda investe la spiaggia proprio quando la precedente si è completamente ritirata, determinando un sollevamento maggiore.

Chi ha visto il film “Interstellar” ricorderà le enormi maree prodotte dal buco nero sulla superficie di quel pianeta (com'è che si chiamava?) visitato da Cooper e compagni; ma la trovata era a mio avviso solo in parte plausibile da un punto di vista scientifico, poichè le stesse forze di marea non dovrebbero consentire l'esistenza di pianeti vicini a un buco nero, che li stritolerebbe risucchiandoli. Per non parlare poi delle radiazioni emesse da Gargantua che avrebbero dovuto uccidere in breve l'equipaggio.

Che si può dire invece delle forze di marea sul corpo dello stesso Cooper quando egli va a cadere dentro il buco nero? Qui il film si prende una licenza di sbagliare, perchè il nostro eroe sarebbe stato allungato e stritolato dalle forze mareali secondo un processo che gli americani chiamano spaghettification.

Secondo il buon Albert le maree sono una manifestazione della curvatura dello spazio-tempo, che ha una geometria iperbolica. In questa pagina viene approfondito l'argomento e calcolata la curvatura associata a una massa $M$.

Direte voi: che c'azzecca questo argomento con la Relatività? Perchè non vi chiedete che c'azzeccano le nascite con la Luna? Ve lo dice il CICAP in questa pagina.

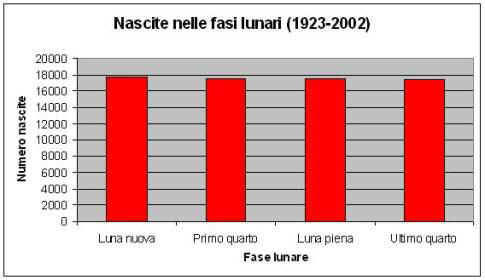
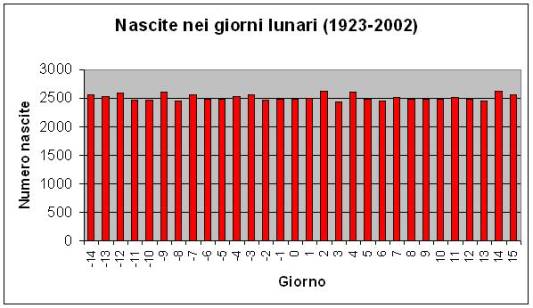
Ecco il risultato della statistica: le nascite nei comuni di Cuneo e Savigliano nell'arco di 80 anni non dipendono asssssolutamente dalle fasi lunari!

• Determinare il rapporto tra le forze di marea lunari e solari.
• Qual è l'accelerazione (dovuta all'effetto di marea, s'intende) a cui è sottoposta una massa di prova sulla ISS?
• A parte il sollevamento delle acque quali possono essere gli effetti, anche a lunghissimo termine, delle maree sulla Terra e sulla Luna?
• Perchè la Luna volge sempre la stessa faccia alla Terra?
• Perchè dobbiamo continuare a dire “The dark side of the Moon”? Che c'è di sbagliato in questa dicitura? Forse è l'unica pecca dell'album dei Pink Floyd

• Questa pagina non ci sarebbe, e certamente io sarei un altro insegnante in questa materia, senza le lezioni di: Elio Fabri, Insegnare Relatività nel XXI secolo, Lez. 10