Questa è una vecchia versione del documento!
Dinamica cosmologica (un cenno al modello classico del Big Bang)
In questa pagina ci proponiamo di fare delle previsioni sull'evoluzione dell'universo, o meglio su quale forma possa avere la funzione $R(t)$, che rappresenta il raggio di curvatura dell'universo, detto anche fattore di scala. Come dici? Perchè fattore di scala? Innanzitutto perchè il termine raggio poco si addice a un eventuale universo piatto o iperbolico, e poi perchè con la misura del redshift $z$ abbiamo informazioni sul rapporto tra il valore di $R_e$ all'istante in cui la radiazione osservata è stata emessa e il suo valore all'epoca attuale $R_r$:
\begin{equation} 1+z = \frac{R_r}{R_e} \end{equation}
Quindi se ad esempio $z=4$ l'universo era $5$ volte più piccolo quando la radiazione è stata emessa; ecco perchè lo si potrebbe anche chiamare fattore di scala. Certo, se si trattasse di un universo sferico potremmo ben chiamarlo raggio dell'universo.
Doveroso maniavantismo iniziale
Le vere equazioni di Einstein non sono quelle che stiamo andando a scrivere. Per farlo ci vorrebbe una matematica universitaria molto complessa. Scriveremo un qualcosa che vi assomiglia un po' e che abbia una lettura non dissimile, ma la dimostrazione che faremo noi non sarà molto rigorosa; servirà solo per dare un minimo di giustificazione a una formula. Ciò non significa però che le vere equazioni non abbiano un solido basamento teorico.
Ci devono essere chiari i nostri obiettivi: a noi interessa solo leggere queste equazioni con gli occhi e con gli occhiali di un fisico e cercare di capire cosa ci suggeriscono riguardo all'evoluzione passata e futura del nostro universo, essendo consapevoli dei limiti della teoria a causa delle misure incerte di $H$ e della densità media dell'universo $\rho$. C'è anche da dire che quei pazzerelli dei fisici teorici ne inventano una al giorno e le cose che diciamo qui andrebbero ancor di più prese con le… pinze? le molle? non mi ricordo più come si dice, ma ci siamo capiti. Insomma la teoria dell'universo inflazionario, la scoperta della materia oscura e dell'energia oscura sono cose che nel corso di questi ultimi anni hanno rivisto, e non di poco, la teoria classica del Big Bang, che è quella di cui cerchiamo di parlare qui e che è la sola di cui si può parlare in una classe di liceo.
Ma ora basta con le ciance, spegnere i cellulari, abbassiamo le luci e iniziamo.
Notazione usata
Anzi no. Prima una cosa importante riguardo alla notazione usata. Se io scrivo:
$$ R''^2 $$
cosa leggete voi? Ammetterete che non è chiaro. È $R$ elevato $112$? È forse la derivata seconda di $R$ elevata al quadrato? Si volevo intendere proprio quest'ultima cosa. Per evitare simili problemi grafici, e quando la derivata è intesa rispetto alla variabile tempo $t$, possiamo trovar scritto anche:
$$ \dot R, \ddot R $$
per intendere rispettivamente la derivata prima, seconda etc. rispetto alla variabile $t$. Così faremo anche noi. Beccatevi quest'altra ciliegina 
Ora iniziamo veramente.
Le equazioni di evoluzione
Come detto prima vogliamo teorizzare su come possa esser fatta la funzione $R(t)$. Con la dicitura “equazioni di evoluzione” intendiamo proprio le equazioni che involvono (è un inglesismo o si può dire? corriggerò…) $R(t)$ e le sue derivate.
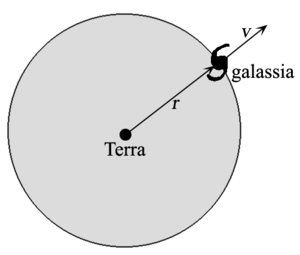
Siamo sulla Terra e dal nostro punto di vista abbiamo una bella sfera di materia di raggio $r$ con densità media uniforme e nel bordo di questa sfera c'è una galassia di massa $m$. Se la sfera non è troppo grande le velocità di allontanamento delle galassie da noi non sono elevate in confronto a $c$ e possiamo usare la fisica classica e la legge della gravitazione universale di Newton, sapendo che, per il teorema di Gauss, la forza di gravità avvertita da $m$ è dovuta solo alla massa interna alla sfera (il teorema di Gauss vale tanto per la legge di Coulomb che per la legge di Newton in conseguenza del fatto che hanno la stessa struttura matematica):
$$ ma = - \frac{GMm}{r^2} $$
Il meno è per via della forza attrattiva, che produce una decelerazione. Qui $M$ è la massa distribuita uniformemente nella sfera, fatta di polveri e stelle. La densità $\rho= M/V$ di materia è da supporsi costante per via del Principio Cosmologico. Scriviamo però l'accelerazione $a$ come derivata seconda di $r$ rispetto al tempo e semplifichiamo $m$:
$$ \ddot r = - \frac{GM}{r^2} $$
È meglio lavorare con la densità $\rho$ anzichè con la massa, quindi l'equazione precedente può essere semplificata:
$$ \begin{cases} M = \rho V \\ V = \dfrac{4}{3}\pi r^3 \\ \ddot r = - \dfrac{GM}{r^2} \end{cases} $$
risolvendo troviamo:
\begin{equation} \label{2} \tag{2} \ddot r = -\dfrac{4}{3}\pi G\rho ~ r \end{equation}
Immagino che vi starete chiedendo che ci frega a noi della distanza $r$ dalla Terra se siamo interessati a studiare il raggio di curvatura (fattore di scala) $R$ dell'universo. Quindi cambiamo subito variabile, ricordando che, in coordinate comoventi, se $\theta$ è la separazione angolare tra la Terra e la galassia, la loro distanza $r$ è la lunghezza dell'arco ed $R$ è il raggio dell'universo:
\begin{equation} \tag{3} \label{3} r=R ~\theta \end{equation}
e ricorderete che tanto per fissare le idee stiamo facendo finta che l'universo sia una superficie sferica a due dimensioni, mentre in realtà ha una dimensione spaziale in più, e non è nemmeno detto che sia sferico.
Andiamo a sostituire la $\eqref{3}$ nella $\eqref{2}$ tenendo presente che:
$$ r=\theta R \\ \dot r = \theta \dot R \\ \ddot r = \theta \ddot R $$
Questo perchè $\theta$ è una costante. Quindi $\theta$ si elide membro a membro e abbiamo:
\begin{equation} \tag{4} \label{4} \ddot R = -\dfrac{4}{3}\pi G\rho ~ R \end{equation}
Prima l'avevo detto che il ragionamento non era rigoroso e immagino che alcuni di voi abbiano già protestato per il poco rigore dovuto al fatto che anche la materia esterna a quella della sfera produce attrazione, visto che l'universo non ha centri. Inoltre non possiamo calcolare le distanze in modo euclideo se non sappiamo ancora se esso è curvo o no. Ma pazienza, abbiamo detto sopra che il nostro obiettivo è speculare sull'equazione di evoluzione, piuttosto che ricavarla con rigore, cosa impossibile per noi, e infatti ci sono dei piccoli ritocchi in arrivo, ma li vediamo fra un attimo.
La densità dipende da $t$
Nell'equazione $\eqref{4}$ non solo $R$ dipende da $t$ (avremmo dovuto scrivere $R(t)$ ma non l'abbiamo fatto per brevità), ma anche $\rho$; l'universo si espande mentre la materia è sempre la stessa (umh… non è detto però… potrebbe trasformarsi in energia, che per la Relatività ha anch'essa un'inerzia e quindi contribuisce alla “gravità”, ma ci torniamo dopo) e quindi la densità diminuisce con il volume, quindi come $1/R^3$.
Se indichiamo con $\rho_0$ la densità all'epoca attuale possiamo scrivere, visto che la densità è inversamente proporzionale a $R^3$:
\begin{equation} \label{5} \tag{5} \frac{\rho}{\rho_0} = \frac{R^3_0}{R^3} \end{equation}
Sostituiamo nella $\eqref{4}$
\begin{equation} \label{6} \tag{6} \ddot R = -\frac{4}{3} \pi G \rho_0 R^3_0 \cdot \frac{1}{R^2} \end{equation}
Si vede che la derivata seconda è negativa, quindi il grafico è concavo e deve essere esistito un istante in cui $R=0$ (il Big Bang), ovvero la curva tocca l'asse delle ascisse.
Chiamatela pure equazione differenziale, visto che contiene sia la funzione che la sua derivata (seconda in questo caso). È talmente facile da risolvere che tra qualche settimana vi farà il solletico. Anzi, risolviamola oggi, tanto sapete già integrare; perchè per togliere la derivata ci vuole la sua operazione inversa, l'integrale, giusto? Giusto.
Via con l'integraluccio allora
Per motivi che saranno chiari tra poco, vogliamo una versione della $\eqref{6}$ in cui compare la derivata prima $\dot R$ anziche $\ddot R$. Anzi diciamolo subito: vogliamo metter dentro la costante di Hubble, che è ciò che poi si misura, la quale dipende da $\dot R$ secondo la relazione:
$$ H = \frac{\dot R}{R} $$
Moltiplichiamo allora per $\dot R$ membro a membro:
\begin{equation} \label{7} \tag{7} \dot R \ddot R = -\frac{4}{3} \pi G \rho_0 R^3_0 \cdot \frac{1}{R^2} \dot R \end{equation}
Ma siccome
$$\dot R = \frac{dR}{dt}$$
moltiplichamo tutto per $dt$ e abbiamo
\begin{equation} \label{8} \tag{8} \dot R \ddot R ~dt = -\frac{4}{3} \pi G \rho_0 R^3_0 \cdot \frac{1}{R^2} ~dR \end{equation}
Ma guardate bene il primo membro: $\ddot R$ è la derivata di $\dot R$, quindi è come scrivere:
$$ \dot R ~\ddot R ~dt = \dot R ~\frac{d\dot R}{dt} dt = \dot R ~d\dot R $$
Usiamo quanto sopra a primo membro e integriamo, portando anche fuori dall'integrale le costanti:
\begin{equation} \label{9} \tag{9} \int \dot R ~d\dot R = -\frac{4}{3} \pi G \rho_0 R^3_0 \int \frac{1}{R^2} ~dR \end{equation}
Non fatevi confondere dal punto sopra la variabile $R$; l'integraluccio a sinistra è come $\int xdx = x^2/2$, mentre quello a destra è come $\int x^{-2}dx = -1/x$ quindi
\begin{equation} \label{10} \tag{10} \dot R^2 = \frac{8}{3} \pi G \rho_0 R^3_0 \cdot \frac{1}{R} + cost \end{equation}
Nelle vere equazioni di Einstein, quelle corrette ottenute con un procedimento più rigoroso, la costante di integrazione non è qualunque, ma si scrive come $-kc^2$ dove $k$ è la curvatura dell'universo.
In particolare abbiamo:
\begin{equation} \label{11} \tag{11} \begin{cases} k=0 \ \ \mbox{spazio euclideo piatto} \\ k=1 \ \ \mbox{spazio sferico} \\ k=-1 \ \ \mbox{spazio iperbolico} \end{cases} \end{equation}
Riscriviamo quindi l'espressione definitiva dell'equazione di evoluzione, che ci dice la legge con cui si evolve il fattore di scala $R$:
\begin{equation} \label{12} \tag{12} \dot R^2 = \frac{8}{3} \pi G \rho_0 R^3_0 \cdot \frac{1}{R} - kc^2 \end{equation}
Entrano in gioco $H$ e la densità critica
Le cose si semplificano se teniamo conto di come si può scrivere la costante di Hubble:
\begin{equation} \label{12.1} \tag{12.1} H = \frac{\dot R}{R} \end{equation}
Infatti, dividendo membro a membro per $R^2$ la $\eqref{12}$ diventa
\begin{equation} \label{13} \tag{13} H^2 = \frac{\dot R^2}{R^2} = \frac{8}{3} \pi G \rho_0 R^3_0 \cdot \frac{1}{R^3} - \frac{kc^2}{R^2} \end{equation}
Noi facciamo le misure di $H$ e della densità dell'universo al tempo odierno, quindi riscriviamo l'equazione al tempo $t_0$ (oggi) in cui $R=R_0$ e $H=H_0$ (anche $H$ come sappiamo dipende da $t$):
\begin{equation} \label{14} \tag{14} H^2_0 = \frac{8}{3} \pi G \rho_0 - \frac{kc^2}{R^2_0} \end{equation}
che si può scrivere anche così
\begin{equation} \label{15} \tag{15} 1 = \frac{\rho_0}{3H^2_0/8\pi G} - \frac{kc^2}{R^2_0 H^2_0} \end{equation}
L'$1$ a sinistra è adimensionale, così, perchè l'equazione sia omogenea nelle dimensioni fisiche, lo devono essere anche gli altri termini. In particolare la quantità a denominatore della prima frazione ha le dimensioni di una densità. Per ragioni che chiariremo tra un attimo chiamiamola densità critica $\rho_c$:
\begin{equation} \label{16} \tag{16} \rho_c = 3H^2_0/8\pi G \end{equation}
e definiamo il parametro di densità $\Omega$ come:
\begin{equation} \label{17} \tag{17} \Omega = \frac{\rho_0}{\rho_c} \end{equation}
Quindi la \eqref{15} si può scrivere
\begin{equation} \label{18} \tag{18} 1 = \Omega - \frac{kc^2}{R^2_0 H^2_0} \end{equation}
che ci consente di calcolare la curvatura $k$:
\begin{equation} \label{19} \tag{19} k = \dfrac{R^2_0 H^2_0}{c^2} (\Omega -1) \end{equation}
E ora dateci gli occhiali del fisico!
Che leggerebbe un fisico qui? Perchè l'ha scritta così, mettendo in rilievo il rapporto $\Omega$ tra la densità attuale (misurabile!) $\rho_0$ e la densità critica $\rho_c$? Che ruolo giocano la densità critica e il parametro $\Omega$? E la costante di Hubble?
Vedete che il segno di $k$ e quindi la curvatura (ovvero la geometria, la sua forma, e tra poco vedremo anche la sua storia passata e futura) dipendono da $\Omega$:
\begin{equation} \begin{cases} \Omega = 1 \ \ (\rho_0=\rho_c) \implies k=0 \ \ \implies \ \ \mbox{universo piatto ed euclideo} \\ \Omega > 1 \ \ (\rho_0>\rho_c) \implies k>0 \ \ \implies \ \ \mbox{universo sferico e chiuso} \\ \Omega < 1 \ \ (\rho_0<\rho_c) \implies k<0 \ \ \implies \ \ \mbox{universo iperbolico ed aperto} \end{cases} \end{equation}
Da questo si capisce l'importanza di conoscere la densità media dell'universo, che si può determinare stimando la massa delle galassie lontane e il numero medio di galassie per unità di volume. Nel contempo è necessario far luce anche sul problema della materia oscura e dell'energia oscura, attore quest'ultimo entrato nel palcoscenico della cosmologia molto di recente. La partita si gioca non soltanto sulle scrivanie dei cosmologi, ma anche in quelle dei fisici teorici e sperimentali che si occupano rispettivamente di fare e verificare le teorie sulle particelle, la teoria delle stringhe per esempio.
Il destino dell'universo
Sfruttando la $\eqref{19}$, l'equazione $\eqref{12}$ si può scrivere
\begin{equation} \label{22} \tag{22} \dot R^2 = H^2_0 R^2_0\left(\Omega\frac{R_0}{R}+1-\Omega \right) \end{equation}
Ora vediamo di farne il limite per $R \longrightarrow + \infty$ per capire cosa succederà in un futuro remoto. Il primo termine dentro la parentesi tende a zero, dunque possiamo stimare con quale velocità l'universo assumerà eventualmente un raggio infinito:
\begin{equation} \label{23} \tag{23} \dot R^2 = H^2_0 R^2_0(1-\Omega) \end{equation}
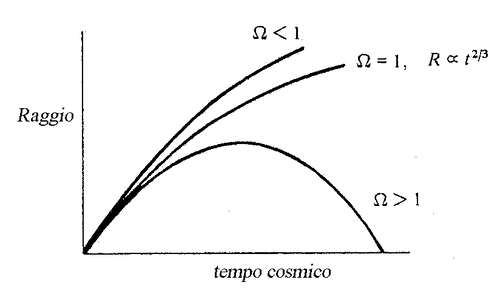
Se $\Omega <1$ ($\rho_0<\rho_c$, geometria iperbolica) l'universo finirà con una velocità finita diversa da zero.
Se $\Omega >1$ ($\rho_0>\rho_c$, geometria sferica) la velocità di espansione $\dot R$ diventerà zero prima che il raggio sia infinito e quindi ricollasserà in una singolarità (lo chiamano Big Crunch) dove $R=0$.
Se $\Omega =1$ ($\rho_0=\rho_c$, geometria euclidea e spazio piatto) l'universo si espande fino ad avere un raggio infinito arrivando a questo stadio con una velocità nulla. Qui c'è una chiara analogia con la velocità di fuga.
In quest'ultimo caso ($\Omega=1$) abbiamo una soluzione della $\eqref{22}$ abbastanza semplice:
\begin{equation} \label{24} \tag{24} \dot R^2 = \frac{H^2_0 R^3_0}{R} \end{equation}
Prima di integrare e risolvere l'equazione differenziale è necessario estrarre la radice
$$\dot R = \frac{H_0 \sqrt{R^3_0}}{\sqrt{R}}$$
e separare le variabili $R$ e $t$, tenendo a mente che $\dot R = dR/dt$:
$$ \sqrt{R}~dR = H_0 \sqrt{R^3_0}dt$$
che è pronta ad essere integrata
\begin{equation} \label{25} \tag{25} \int_0^R \sqrt{R}~dR = H_0 \sqrt{R^3_0} \int_0^t dt \\ \implies \frac{R^{3/2}}{3/2} = H_0 \sqrt{R^3_0} ~ t \\ \implies R = R_0 \left(\frac{3}{2}H_0 t\right)^\frac{2}{3} \end{equation}
La dinamica di questi tre tipi di comportamento è schematizzata nella figura qui sotto:
L'universo dominato dalla radiazione
Nel discorso fatto sin qui, abbiamo immaginato un universo che si espande decelerando, a causa della mutua attrazione gravitazionale tra le sue parti. Abbiamo per il momento immaginato che solo la materia, fatta in maggioranza di protoni e neutroni (sotto forma di idrogeno ed elio), concentrata nelle stelle, sia responsabile della forza di gravità. Ma la relatività di Einstein ci dice che anche la radiazione elettromagnetica è inerzia, ed è in grado di incurvare lo spazio. Da qui la seguente questione:
- Abbiamo visto che la densità di materia $\rho_m$ diminuisce con il cubo del raggio: $\rho_m \propto 1/R^3$
- In che modo la densità dei fotoni (energia dei fotoni per unità di volume) $\rho_f$ decresce con $R$?
- Oggi le misure ci dicono che $\rho_f \approx 0,001 \rho_m$, ovvero, come si suol dire, l'universo è dominato dalla materia.
- Vi è mai stata un'epoca passata in cui vi erano più fotoni che particelle, ovvero $\rho_f>\rho_m$?
Vedremo tra un attimo che la risposta è sì, ovvero deve essere esistita la cosiddetta “palla di fuoco” (fireball). Ecco il ragionamento che lo dimostra.
Indichiamo appunto con $n$ il numero di fotoni per unità di volume e con $\epsilon$ la loro energia media. Allora la densità dei fotoni (energia per unità di volume) è:
\begin{equation} \label{26} \tag{26} \rho_f = n\epsilon \end{equation}
Per via dell'aumento di volume dell'universo, dovrebbe essere chiaro (o no?) che $n$ diminuisce come $R^3$:
\begin{equation} \label{27} \tag{27} n \propto \frac{1}{R^3} \end{equation}
Chiediamoci se l'energia dei fotoni $\epsilon$ varia anch'essa con l'espansione dell'universo. Sappiamo già da quando siamo nati che quest'energia è proporzionale alla frequenza:
$$\epsilon = hf$$
dove $h$ è la famosa costante di Planck. E sappiamo da ancor prima di esser nati che la frequenza è inversamente proporzionale alla lunghezza d'onda:
$$f=\frac{c}{\lambda}$$
Quindi l'energia del fotone si può scrivere
$$ \epsilon = \frac{hc}{\lambda} $$
E siccome avevamo scoperto che la lunghezza d'onda della luce ricevuta è proporzionale a $R$:
$$ \frac{\lambda_r}{\lambda_e} = \frac{R_r}{R_e} $$
possiamo asserire che l'energia del fotone è inversamente proporzionale ad $R$:
\begin{equation} \label{28} \tag{28} \epsilon \propto \frac{1}{R} \end{equation}
Sostituendo la $\eqref{28}$ e la $\eqref{27}$ nella $\eqref{26}$ ne deduciamo che:
\begin{equation} \label{30} \tag{30} \rho_f \propto \frac{1}{R^4} \end{equation}
mentre ricordiamo che
\begin{equation} \label{31} \tag{31} \rho_m \propto \frac{1}{R^3} \end{equation}
Che significa ciò (inforchiamo di nuovo gli occhiali del fisico)? $\rho_m$ decresce più lentamente di $\rho_f$, e questo giustifica il fatto che oggi l'universo è “dominato dalla materia”, come si suol dire, ma se torniamo indietro nel tempo ($R \longrightarrow 0$) si capisce che vi deve essere stato un tempo prima del quale $\rho_f>\rho_m$ (la palla di fuoco) dove l'universo doveva essere fatto soprattutto di fotoni. Ovvero l'universo all'inizio era fatto solo di radiazione.
Si stima che il tempo in cui $\rho_f=\rho_m$ sia dell'ordine di circa dieci milioni di anni dal Big Bang.
La radiazione cosmica di fondo
I fotoni della cosiddetta “palla di fuoco” sono ancora in giro per l'universo e noi li possiamo osservare; l'universo ha una densità media bassissima ($\sim 10^{-30} g/cm^3$), ciò significa che è praticamente vuoto e quindi trasparente al passaggio della luce, che solo di rado interagisce con la materia.
Questa radiazione di fondo si chiama così perchè proviene da ogni direzione in egual misura (fino a una parte su $100.000$), a riprova del fatto che l'universo è isotropo. Ma come facciamo a distinguere quei fotoni provenienti dal lontano Big Bang da quelli emessi da una stella qualunque?
Ci sono delle relazioni fisiche fuori dalla nostra portata (abbastanza semplici, ma non abbiamo il tempo), che dicono che l'energia media del fotone è legata alla temperatura $T$ del corpo che la emette (si dovrebbe dire “corpo nero”, ma tralasciamo questo dettaglio) da una semplice relazione di proporzionalità:
\begin{equation} \label{32} \tag{32} \epsilon = kT \end{equation}
dove $k$ è una costante chiamata costante di Boltzmann.
Orbene, poichè già sappiamo dalla $\eqref{32}$ che $\epsilon \propto 1/R$ ne vien fuori che:
\begin{equation} \label{33} \tag{33} T \propto \frac{1}{R} \end{equation}
come è anche intuitivo che sia, ovvero più l'universo si espande e più si raffredda e viceversa. I modelli cosmologici sono in grado di predire qual è il raggio attuale $R$ dell'universo e quindi la sua temperatura $T$ e con essa la lunghezza d'onda dei fotoni della radiazione di fondo.
La cosa bella è che le osservazioni confermano queste previsioni, perchè la radiazione di fondo si presenta esattamente come le equazioni dicono che deve essere, ovvero con una frequenza di $160,2~ GHz$ corrispondenti ad una lunghezza d'onda di $1,9~ mm$ (microonde). Ciò corrisponde a una temperatura media dell'universo di circa $3K$.
La radiazione cosmica di fondo è stata prevista nel 1948 da George Gamow, Ralph Alpher, e Robert Herman ed è stata osservata per la prima volta nel 1964. È isotropa fino a una parte su 100.000. La sua effettiva osservazione è un grande risultato per la teoria e conferma che anche il principio cosmologico è fondato.
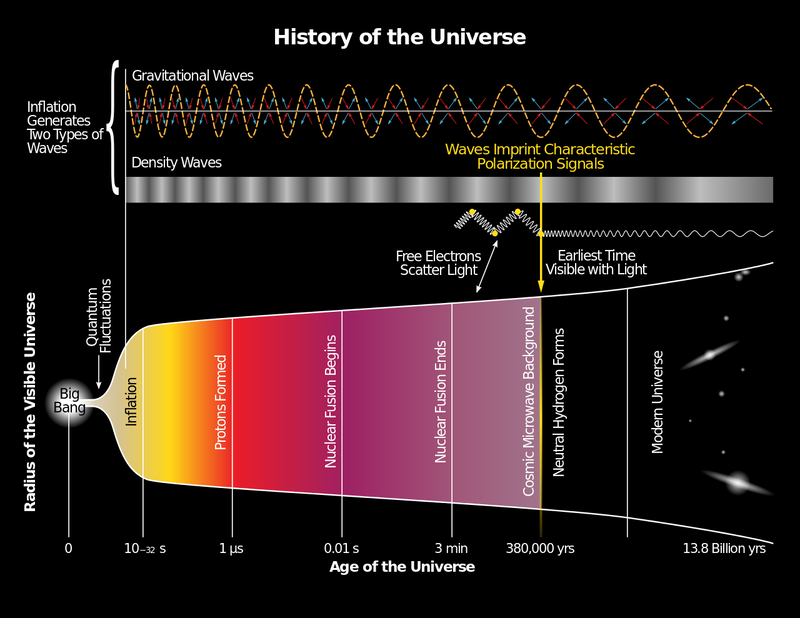
Per una cronistoria dell'evoluzione del Big Bang e per sapere qualcosa di più sulla radiazione di fondo si vedano i riferimenti in fondo a questa pagina.
Cosa dicono i dati reali? Quali sono i problemi aperti?
I dati più recenti sembrano indicare che:
- L'età dell'universo è di circa $13,8$ miliardi di anni
- I dati su $\rho$ sembrano indicare una geometria iperbolica ($k=-1$)
- I dati basati sul redshift e le distanze delle galassie indicano invece un universo piatto ($k=0$)
- L'universo si espande ora in modo accelerato, come se vi fosse una misteriosa forma di energia oscura per cui le masse si respingono anzichè attrarsi.
Rimane da capire come mai, nonostante l'espansione iniziale, l'universo appaia così isotropo e uniforme. C'è anche da capire di cosa sia fatta la materia oscura e quale sia la natura dell'energia oscura.
Un altro enigma è questo. Se l'universo inizialmente era fatto solo di fotoni, e questi hanno creato la materia producendo coppie particella-antiparticella, ad esempio:
$$ \gamma + \gamma \longrightarrow e^- + e^+$$
in cui due fotoni $\gamma$ producono un elettrone e un positrone (l'anti-elettrone), la materia e l'antimateria sono state prodotte in uguale quantità. Ma allora dov'è finita l'antimateria? Perchè sembra non avere diritto di esistenza stabile nel nostro universo?