Questa pagina riprende la lezione 10 del libro di E. Fabri Insegnare Relatività nel XXI secolo, al fine di semplificare gli aspetti matematici e rendere accessibile l'argomento ai miei studenti della scuola secondaria superiore.
Curvatura dello spazio tempo
Chi arriverà in fondo a questa pagina riuscirà a calcolare la curvatura dello spazio-tempo vicino a una massa $M$.

Osservando i diagrammi spazio-temporali, in due diverse occasioni, abbiamo avuto una premonizione: lo spazio-tempo è curvo; non può essere ben rappresentato su un piano $s-t$. Una di queste circostanze è stato lo studio delle maree, che in questa pagina approfondiremo; sai ricordare tu qual è stata l'altra?
Le maree viste nello spazio-tempo
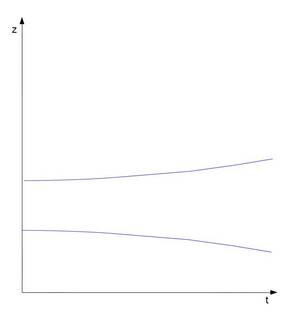
Abbiamo ormai imparato che in un riferimento in caduta libera vi sono pur sempre le forze di marea che separano due masse lasciate libere di fluttuare. Nel diagramma $s-t$ abbiamo due linee parallele che divergono, e questo ci suggerisce che le cose vanno diversamente dalla geometria euclidea che ci è familiare.
Einstein interpreta ciò in termini di curvatura dello spazio-tempo: se non ci fosse la gravità (e quindi le forze di marea) le due masse non cambierebbero la loro distanza e nello $s-t$ le due rette parallele non divergerebbero (che brutta parola! si può dire diverg…? bah). Ma lo spazio-tempo è curvo ed esse non stanno ferme pur non essendo soggette a forze. La curvatura è introdotta dalla massa che ha generato il campo gravitazionale.
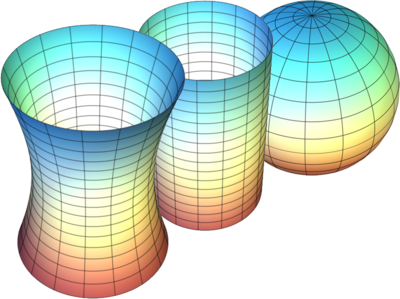
Ma se lo spazio-tempo è deformato e non è piano, com'è fatto? Che forma ha? Di solito si illustra il concetto con figure come questa, che però non rappresenta la vera geometria (la forma) dello spazio-tempo.
I matematici descrivono la geometria di uno spazio con un numero, il raggio di curvatura $R_C$, e dalla curvatura, di cui parleremo tra poco. Se lo spazio è una sfera il raggio di curvatura non cambia da punto a punto e nemmeno al variare della sezione considerata, e corrisponde al suo raggio; invece in un piano non c'è curvatura, come dire che il raggio di curvatura è infinito.
La curvatura di una sfera
Per familiarizzare con il concetto di curvatura mettiamoci su una sfera, che è uno spazio curvo a noi familiare. É una superficie bidimensionale, che è incurvata nella terza dimensione. Di certo delle formiche che si muovessero su una mela sferica non percepirebbero questa dimensione aggiuntiva, ma potrebbero pur sempre fare delle misure geometriche per scoprire che lo spazio su cui vivono non è piatto ma sferico: ad esempio potrebbero scoprire che la somma degli angoli interni a un triangolo è maggiore di $180°$, o che la lunghezza di una circonferenza è minore di $2\pi r$.
Come misurare il raggio $R$?
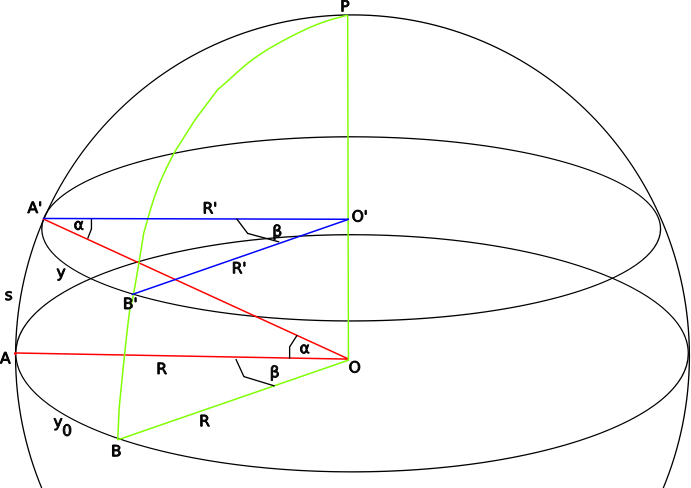
Vediamo come si potrebbe misurare $R$ stando ancorati alla sfera, proprio come le formiche, che non possono uscire nella terza dimensione. Qui le linee di minima distanza (geodetiche) non sono linee rette, ma archi di cerchio massimo.
Disegnamo il triangolo sferico $ABP$. Da due punti $A$ e $B$, sullo stesso parallelo, tracciamo le distanze dal polo $\widehat{AP}$ e $\widehat{BP}$. Queste distanze, uguali tra loro, sono archi di cerchio massimo, cioè delle geodetiche. Quando su $\widehat{AP}$ si percorre un tratto curvilineo di lunghezza $s$, si perviene in $A'$; allo stesso modo da $B$ si giunge in $B'$. Ora, la distanza $\widehat{A'B'}$ è approssimativamente uguale all'arco di cerchio di raggio $R'$. Dico approssimativamente perchè questo NON è un cerchio massimo, ma possiamo trascurare l'errore se consideriamo l'angolo diedro $\beta$ abbastanza piccolo.
La distanza $y_0$ tra $A$ e $B$, nel viaggio verso il polo, è diventata $y=\widehat{A'B'}$, che è minore di $y_0$ perchè ci stiamo muovendo su una sfera. Noi vogliamo scoprire con quale legge varia $y$, che è la distanza tra due geodetiche, e nel contempo misurare il raggio di curvatura $R$.
L'angolo $\beta$ in radianti è dato dal rapporto tra la lunghezza dell'arco e il raggio. Quindi lo possiamo calcolare sia sulla circonferenza di centro $O$ che in quella di centro $O'$:
\begin{equation} \label{1} \beta = \frac{y}{R'} = \frac{y_0}{R} \end{equation}
perciò, notando che dal triangolo $OO'A'$ è $R'=R \cos \alpha ~$ la $\eqref{1}$ diventa:
\begin{equation} \label{2} y = y_0 \frac{R'}{R} = y_0 \cos \alpha = y_0 \cos (s/R) \end{equation}
Nell'ultima uguaglianza, essendo l'arco $\alpha$ espresso in radianti, esso può essere scritto come il rapporto tra l'arco $s$ e il raggio $R$.
Calcoliamo ora la derivata seconda di
\begin{equation} \label{3} y = y_0 \cos (s/R) \end{equation}
rispetto a $s$ ($R$ è costante):
$$ y'(s) = - y_0 \frac{1}{R} \sin (s/R) \qquad \implies \qquad y''(s) = -y_0 \frac{1}{R^2} \cos (s/R)$$
L'ultimo membro è proprio uguale a $y$ moltiplicato per $-1/R^2$, quindi:
$$ y''(s) = - \frac{1}{R^2} y $$
e da qui esplicitiamo $R$
\begin{equation} \label{4} \frac{1}{R_C^2} = -\frac{1}{y} y''(s) \end{equation}
In quest'ultima formula ho messo $R_C$ al posto di $R$ per intendere il raggio di curvatura $R_C$, che ci servirà per definire la curvatura di Gauss di una superficie qualunque. Il fatto che il calcolo qui fatto lo si possa generalizzare a un qualunque tipo di superficie lo dobbiamo a Gauss.
Il primo membro della $\eqref{4}$ ha segno positivo, ma anche il secondo membro, nonostante il segno $-$. Infatti la derivata seconda è anch'essa negativa; per convincerci di ciò è sufficiente ricordare che la funzione $\eqref{3}$, per valori piccoli di $s$, ha la concavità rivolta verso il basso e perciò la $y''$ è negativa.
Sto enfatizzando il fatto che la curvatura della sfera è positiva perchè tra poco vedremo che la geometria dello spazio-tempo è simile alla geometria iperbolica, tipica di una superficie a sella, che invece ha curvatura negativa.
Ma intanto avrete notato che sto parlando di curvatura come sinonimo della quantità $1/R_C^2$. Per una definizione rigorosa del concetto di curvatura di Gauss vedere i riferimenti indicati in fondo a questa pagina.
Ricapitolando, cosa rappresenta la funzione $y = y_0 \cos (s/R)~$ o, il che è lo stesso, la $\eqref{4}$? È la legge secondo cui le geodetiche che ci conducono verso il polo diminuiscono la distanza reciproca. Dovrebbe essere chiaro a questo punto che questa legge deve dipendere dal raggio di curvatura $R_C$: tanto più è piccolo $R_C$ quanto più velocemente esse convergono e viceversa.
La curvatura dello spazio-tempo
Torniamo ora alla relatività e cerchiamo di utilizzare la $\eqref{4}$ per calcolare il raggio di curvatura dello $s-t$ vicino a una massa $M$. Riprendiamo la formula (1) del campo di marea già derivata nella pagina sulle maree:
\begin{equation} \label{5} g(z) = \frac{2GM}{R^3}z \end{equation}
Come dite? Non somiglia per niente alla $\eqref{4}$? Allora la mettiamo meglio a fuoco… per esempio cosa è $g(z)$? È il campo gravitazionale, quindi un'accelerazione, ovvero la derivata seconda dello spazio $z$ rispetto al tempo $t$:
\begin{equation} \label{6} g(z) = z''(t) = \frac{2GM}{R^3}z \end{equation}
È bene ricordare anche una notazione che sotto utilizzeremo per scrivere la derivata seconda:
$$ z''(t) = \frac{d}{dt} \left (\frac{dz}{dt} \right ) = \frac{d^2z}{dt^2} $$
Quindi $g(z)$ è l'accelerazione di una massa di prova $m$. Questa legge ci dice come divergono le due masse, un po' come la $\eqref{4}$ ci dice il modo in cui si avvicinano due geodetiche inizialmente parallele su una sfera. Ecco, cominciamo a guardare le due linee della figura 1 come due geodetiche dello spazio-tempo. Anche qui partono parallele, ma poi che fanno? Divergono! Quindi vanno al contrario rispetto a quanto succede in una sfera… la geometria (leggi volgarmente forma) dello spazio-tempo deve essere diversa da quella di una sfera.
Cerchiamo allora di vederci più chiaro. La $\eqref{6}$ si può scrivere anche così
\begin{equation} \label{7} \frac{2GM}{R^3} = \frac{1}{z} z''(t) = \frac{1}{z} \frac{d^2z}{dt^2} \end{equation}
ora non mi dite che non vedete l'analogia con la $\eqref{4}$ (ed ecco il solito che fa finta di avere la testa dura… 
Aggiustiamo dunque la $\eqref{7}$:
\begin{equation} \label{8} \frac{2GM}{c^2R^3} = \frac{1}{z} \frac{d^2z}{c^2dt^2} = \frac{1}{z} z''(ct) \end{equation}
Quindi dal confronto tra la $\eqref{8}$ e la $\eqref{4}$ possiamo scrivere
\begin{equation} \label{9} \frac{1}{R^2_C} = \frac{2GM}{c^2R^3} \end{equation}
$R_C$ è il raggio di curvatura cercato e non è da confondere con $R$ che è il raggio della massa $M$, la Terra per esempio.
Una differenza importante con il caso della sfera è il segno $-$ della derivata seconda. Nel caso della sfera compare il meno perchè le geodetiche si avvicinano e la curva $y(s)$ è concava (si trattava della funzione coseno per piccoli valori di $s$). Nello spazio-tempo la formula non presenta il $-$, quindi la derivata seconda ha segno positivo; questo è quello che succede quando le geodetiche divergono.
La geometria dello $s-t$ si chiama iperbolica, raffigurata a sinistra nella figura in basso. Per un approfondimento si vedano le referenze in fondo a questa pagina.
Semplifichiamo ancora
La presenza del rapporto $M/R^3$ nella $\eqref{9}$ ci suggerisce di riscrivere la formula facendo comparire la densità $\rho$. Basta introdurre il fattore $4/3$ che abbiamo nella formula del volume della sfera ($V=\frac{4}{3}\pi R^3$)
\begin{equation} \label{10} \frac{1}{R^2_C} = \frac{8\pi}{3}\frac{G}{c^2} \rho \end{equation}
Allora la curvatura prodotta da una massa $M$ dipende solo dalla sua densità. Si capisce che l'implosione di una stella e il conseguente aumento di $\rho$ implica un consistente aumento della curvatura dello spazio-tempo nelle sue vicinanze.
Problemi
- Calcolare $R_C$ per la Terra, per il Sole, per una nana bianca, per una stella di neutroni.
Riferimenti
Approfondimenti
Capolavoro didattico sulle geometrie non euclidee di Paolo Lazzarini (spiegazioni cristalline, con esperimenti e animazioni geogebra). Il primo link è la pagina principale del lavoro.