Moto uniformemente accelerato
Definizione
Moto in cui l'accelerazione è costante. La velocità cresce in modo proporzionale al tempo, quindi il grafico v-t è una retta.
La prima legge del moto uniformemente accelerato
La prima legge esprime come varia la velocità col tempo (dimmi che ore sono e ti dirò a che velocità vai).
Caso con $v_0=0$
Partiamo dalla definizione di accelerazione vista in un'altra pagina:
$$a=\frac{\Delta v}{\Delta t}=\frac{v}{t}$$
La precedente si può scivere anche
$$ v = at $$
Il grafico è una retta uscente dall'origine e l'accelerazione è il coefficiente angolare della retta. La velocità è proporzionale al tempo.
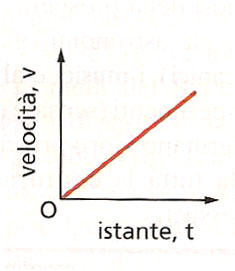
Caso con $v_0\neq 0$
Questa è la definizione di accelerazione vista in un'altra pagina:
$$a=\frac{\Delta v}{\Delta t}=\frac{v-v_0}{t} (con t_0 = 0)$$
La precedente si può scivere anche
$$ v = at + v_0 $$
Il grafico è una retta che non passa per l'origine. L'accelerazione è anche qui il coefficiente angolare della retta.
La relazione è di tipo lineare.

La seconda legge del moto uniformemente accelerato
La seconda legge esprime come varia lo spazio percorso col tempo (dimmi che ore sono e ti dirò dove trovi).
Il ragionamento qui sotto si basa sul fatto che lo spazio percorso in un moto qualunque equivale all'area sottesa dalla curva nel grafico v-t. Se non ti è chiaro il perchè vedi questa pagina.
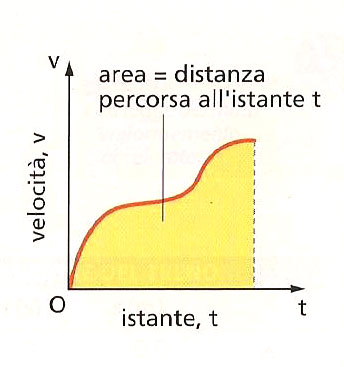
Se ci pensi bene, ciò è abbastanza ovvio nel caso del rettilineo uniforme (velocità costante), il cui grafico v-t è il primo in figura 4. La velocità è costante e la retta non ha pendenza, ovviamente, visto che il suo valore non cambia. Quindi lo spazio, che equivale all'area del rettangolo giallo, si calcola come base(tempo) moltiplicato per l'altezza (velocità, per cui viene fuori la famosa formula che tutti conosciamo:
$$ s = vt $$
Come detto, si può dimostrare che ciò vale sempre, quindi anche nel moto uniformemente accelerato, il cui grafico, nel caso $v_0 \neq 0$, è mostrato in basso in figura.
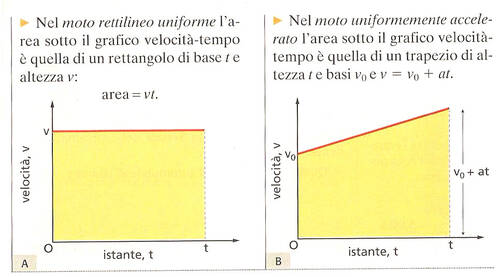
Poichè dobbiamo calcolare l'area del trapezio:
$$ \color{Blue}{Area (spazio)}=\frac{\left( \color{Red}{Base\ maggiore}\ +\ \color{Green}{Base\ minore} \right) \times \left( \color{Maroon}{Altezza} \right)}{2} $$
Osservando bene la figura:
$$ \color{Red}{Base\ maggiore = v} $$
$$ \color{Green}{Base\ minore =v_0} $$
$$ \color{Maroon}{Altezza\ (il\ trapezio\ è\ rovesciato) = t} $$
Quindi:
$$ \color{Blue}{s} = \frac{(\color{Red}{v} + \color{Green}{v_0}) \times \color{Maroon}{t}}{2} $$
Questa però è una equazione provvisoria, poichè contiene 3 variabili (s, v, t): possiamo alleggerirla eliminando la variabile v con l'utilizzo della prima legge del moto ricavata sopra:
$$ \large{ \begin{cases} s = \frac{ ( \color{Red}{v} + v_0 ) \times t }{2} \\ \color{Red}{v} = at + v_0 \end{cases} } $$
Sviluppando i calcoli abbiamo
$$ s = \frac{ (at+v_0 + v_0) \times t }{2} = \frac{ ( at+2v_0 ) \times t }{2} = \frac{at^2 + 2 v_0 t}{2} = \frac{1}{2}at^2 + v_0 t $$
E questa è la forma della legge nel caso $v_0\ \neq 0$
$$ s = \frac{1}{2} at^2 + v_0 t $$
Nel caso in cui il moto parta da fermo $v_0 = 0$, come negli esperimenti da noi eseguiti in laboratorio, abbiamo più semplicemente:
$$ s = \frac{1}{2} at^2 $$
Quindi in un moto uniformemente accelerato con partenza da fermo lo spazio percorso è proporzionale al quadrato del tempo. Ciò dimostra che i moti da noi osservati in laboratorio sono quindi dei moti uniformemente accelerati, poichè abbiamo trovato una legge di questo tipo (vedere questa pagina correlata).
La terza legge del moto uniformemente accelerato
Mettendo a sistema le prime due equazioni viste sopra, eliminando il tempo fra le due, si dimostra la relazione tra la velocità e lo spazio percorso, che può essere utile, per esempio, per determinare la velocità raggiunta dopo un certo spazio percorso:
$$ \large{ \begin{cases} v = v_0 + at \\ s = \frac{1}{2} at^2 + v_0 t \end{cases} } $$
$$ v^2 = v_0^2 + 2as $$
Nel caso di velocità iniziale nulla ($v_0=0$), la precedente diventa:
$$ v^2 = 2as $$