La ricerca della legge del moto uniformemente accelerato
Questa pagina spiega il senso e i risultati degli esperimenti eseguiti in laboratorio con il ben noto apparato sperimentale che tutti conosciamo, ma di cui nessuno, se non la Leybold stessa, conosce il nome. 
Cosa ci proponiamo di fare con questi carrelli e questi nastri?
Prima di studiare il moto accelerato avevamo visto, in una precedente esperienza di laboratorio, che un corpo su cui non agiscono delle forze si muove in linea retta a velocità costante (moto rettilineo uniforme). Questo è il primo principio della dinamica.
Vogliamo ora scoprire cosa succede quando un corpo è soggetto ad una forza che agisce su di esso senza variare la sua intensità durante tutto il moto.
L'esperienza di laboratorio da noi eseguita è iniziata proprio con l'osservazione del moto di un carrello che viene spinto (o trainato) da una forza costante.
Abbiamo realizzato questa situazione ponendo il il carrello in un binario orizzontale, nel quale gli attriti erano minimi, e legandolo ad un peso in caduta. Le accelerazioni osservate dipendevano dal valore di questo peso e dalla massa del carrello stesso.
Ovviamente la forza trainante (costante) può essere proprio il peso del carrello, se il piano viene inclinato. Per questo motivo abbiamo eseguito delle misure anche nel moto sul piano inclinato, eseguendo delle corse al variare dell'inclinazione del piano e della massa del carrello, per scoprire come varia di conseguenza l'accelerazione.
Cosa vogliamo misurare
Scoprire cosa succede è un modo un po' vago di esprimere un obiettivo. Stiamo guardando un carrello che corre e ci sembra che lo spazio percorso dipenda dal tempo, ovviamente. Ma in che modo? Esiste una legge che esprime la relazione tra lo spazio e il tempo? Se sì, questa legge vale sempre, al variare della forza motrice e della massa del carrello?
Sia lo spazio che il tempo sono grandezze fisiche, che possiamo misurare come ben sappiamo leggendo i nostri nastrini (per brevità ometto qui la pappardella su come si fa e sull'apparato sperimentale). Per ciascuna corsa, cercheremo di mettere in relazione lo spazio (variabile dipendente) e il tempo (variabile indipendente) per scoprire la relazione che vi è fra di essi, che in cinematica si chiama legge oraria del moto.
Nella tabella in basso possiamo vedere come abbiamo organizzato i dati sperimentali sul foglio di calcolo, mettendo in colonne affiancate le misure di spazio e di tempo.
Osservando queste “pile” di dati siamo riusciti, come viene spiegato qui sotto, a scrivere la legge oraria del moto che stiamo osservando.
Orizzonti dei nostri esperimenti
…“del moto che stiamo osservando”?! Già, che razza di moto è questo? Scopriremo, come vedremo sotto, che in tutti i moti osservati la relazione tra spazio e tempo è di tipo quadratico, ovvero:
$$s=k \cdot t^2$$
con la costante $k$ che dipende dalle variabili del moto, ovvero la forza motrice e la massa del carrello.
Scopriremo, una volta formalizzato il tutto, che
- questa costante $k$ altro non è che la metà dell'accelerazione costante
- in altre parole il doppio del rapporto $s/t^2$ ci dà l'accelerazione, e quindi l'esperimento del moto sul piano inclinato costituirà un esempio di misura dell'accelerazione di gravità (con le dovute proporzioni, visto che la caduta non è “a piombo”).
- che il moto osservato, se gli attriti sono trascurabili, è uniformemente accelerato
Infine, ma questo è un obiettivo più a lungo termine,
- comprenderemo quali sono i rapporti tra massa (peso?), forza, accelerazione aprendo ai principi della dinamica.
Analisi dei dati
Prendiamo come esempio i dati in questa figura, raccolti da Anna Livia Vigiano (3D, a.s. 2011/2012).

Come si vede, sono state eseguite 3 corse con una forza trainante data da un pesetto attaccato al carrello che aveva un peso via via crescente:
| Peso | |
|---|---|
| 1 corsa | $10,2 g_p$ |
| 2 corsa | $15,2 g_p$ |
| 3 corsa | $20,2 g_p$ |
Invece la massa del carrello, nelle 3 corse, era sempre costante (100 g).
I dati degli esperimenti in cui varia la massa del carrello con il peso trainante costante, e di quelli eseguiti sul piano inclinato sono stati analizzati in modo analogo e portano alle stesse conclusioni.
Come si può vedere dalla figura, il rapporto tra $s$ e $t^2$ appare costante, per lo meno è la colonna con meno variazioni rispetto alle altre.
Anche la prima colonna con il rapporto $s/t$ ha dei valori quasi costanti. Infatti il moto, seppur accelerato, era molto vicino a un moto rettilineo uniforme, dove lo spazio è appunto direttamente proporzionale al tempo.
Naturalmente i rapporti non potranno mai essere uguali per via degli errori sperimentali.
Il grafico s-t
Poichè lo spazio sembra direttamente proporzionale al quadrato del tempo, il grafico è una parabola:
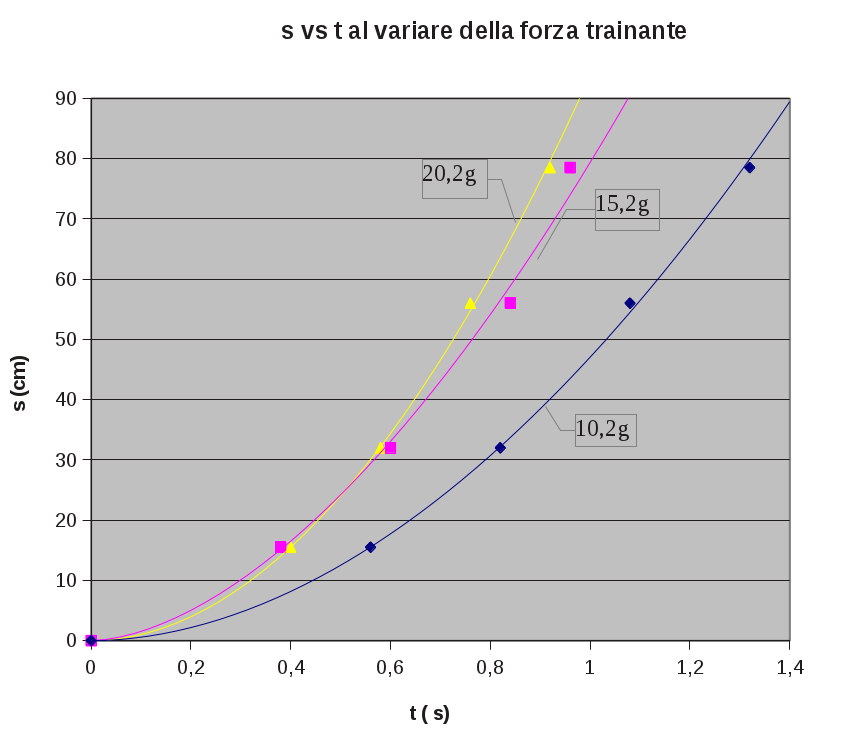
Il grafico $s-t^2$
Se invece guardiamo il grafico $s-t^2$ ci accorgiamo che l'ipotesi che s sia direttamente proporzionale a $t^2$ è alquanto sensata, dal momento che i punti si allineano bene lungo una retta passante dall'origine.
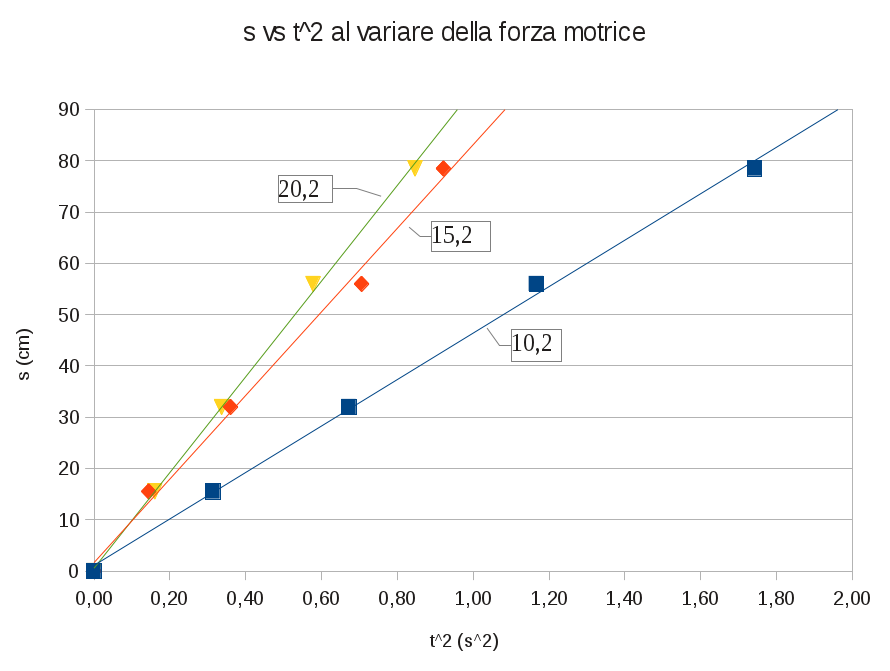
Conclusioni
Alla luce dei nostri dati, anche quelli degli altri esperimenti, sembra che la legge del moto determinato da una forza costante sia:
$$\frac{s}{t^2}=k$$
oppure
$$s=\frac{k}{t^2}$$
Il grafico mostra che le differenze al variare della forza trainante non stanno nella struttura della legge fisica, bensì nel semplice parametro $k$, che determina la pendenza (coefficiente angolare) della retta nel grafico.
Ma la ricerca è appena cominciata...
Già… questo è solo l'inizio, come dicevamo sopra a proposito degli obiettivi della nostra ricerca. Infatti, che cosa ci racconta di tanto importante questa relazione appena trovata?
Nella pagina relativa al moto uniformemente accelerato vedremo che quando $s/t^2=k$ l'accelerazione è costante e che il parametro $k$ è il doppio del valore dell'accelerazione stessa, quindi possiamo anticipare che:
$$s=\frac{1}{2}at^2$$
Pertanto i moti che abbiamo osservato sono esempi di moto uniformemente accelerato, dove la velocità aumenta in modo costante con il tempo.
Non c'è bisogno che io scriva che sei invitato (leggi obbligato) a passare alla pagina sul moto uniformemente accelerato e da questa, se ne hai bisogno, a tutti i preliminari sulla velocità e l'accelerazione (sempre che io abbia già scritto queste altre pagine). In ogni caso usa il libro di testo per quanto riguarda le definizioni preliminari e tutto il resto.