Indice
La relatività del tempo
Abbiamo imparato che la luce ha una velocità costante $c$ in tutti i riferimenti inerziali. Ce lo impone il Principio di Relatività (PR). Questo fatto ha delle immediate conseguenze, che si intuiscono notando che eventi che risultano simultanei in un riferimento non lo sono per un altro che si muove rispetto a questo.
Il treno di Einstein
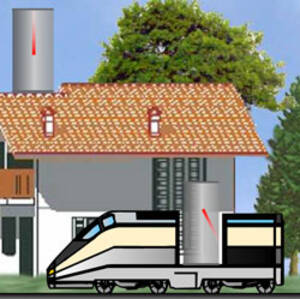
Einstein ci spiega la relatività del tempo con l'esempio del treno (vedere l’animazione su moodle).
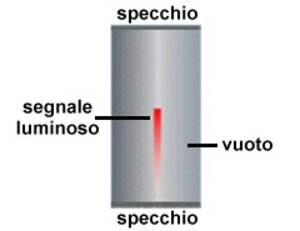
Come si vede ci sono due orologi a luce posti nel treno e nella casa. Vi è un raggio luminoso che “rimbalza” tra due specchi. Lo spazio tra i due specchi è vuoto, sicché la distanza tra di essi vale $c \Delta \tau$, essendo $\Delta \tau$ il tempo impiegato tra un tick e l’altro. Dal momento che $c$ è invariante, l'orologio a luce può essere considerato un orologio universale.
Il tempo proprio
$\Delta \tau$ è l’intervallo di tempo che separa due eventi che avvengono nello stesso luogo: l’emissione e la ricezione avvengono nello stesso luogo perché in questo riferimento il raggio di luce va su e giù senza traslare. Questo tempo si chiama tempo proprio.
Ma perché l'orologio in moto è in ritardo rispetto a quello fermo?
Perché la luce deve percorrere, sempre alla stessa velocità (per il PR), una distanza maggiore. L’effetto si inverte cambiando il sistema di riferimento. Ossia chi guarda le cose dal treno giudica più lento l’orologio posto sulla casa, e viceversa. Ma allora chi ha ragione? Hanno ragione entrambi. Fintanto che i due riferimenti sono inerziali vi è una simmetria tra di essi. Infatti sappiamo che due riferimenti inerziali sono indistinguibili.
Ma allora il paradosso dei gemelli come si spiega? Quando i gemelli si incontrano dopo il viaggio, uno dei due è più vecchio dell'altro. Come si può spiegare questa rottura della simmetria?
Per il momento diciamo che si parla di paradosso non perchè la relatività del tempo è fuori dal senso comune, ma in quanto è necessario dire per quale motivo i due non sono invecchiati allo stesso modo.
La relazione tra i tempi
Tornando a noi, calcoliamo la relazione tra i tempi misurati dai due osservatori. Noi siamo sulla casa e il treno si muove a velocità $v$.
Dobbiamo misurare l’intervallo di tempo tra 2 eventi ben precisi:
- Il raggio di luce dell’orologio posto sul treno in movimento parte dallo specchio superiore;
- Lo stesso raggio giunge sullo specchio inferiore.
Il nostro collega sul treno, chiamiamolo Albert, misura il tempo proprio $\Delta \tau$ tra i due tick.
Ora guardiamo i due eventi dalla casa e misuriamo con il nostro orologio il tempo $\Delta t$ che li separa.
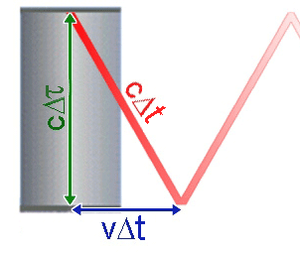
Siccome l’orologio di Albert si muove col treno, noi vediamo la luce fare un tragitto a zig-zag come nella figura.
Con il nostro orologio misurariamo il tempo $\Delta t$ che occorre alla luce per compiere il tragitto obliquo mostrato in rosso, e con il regolo misurariamo la distanza segnata in azzurro.
Evidentemente dovremo avere che $\Delta t > \Delta \tau$ visto che il tratto obliquo è più lungo e viene percorso sempre a velocità $c$. Applicando il teorema di Pitagora si trova la legge della dilatazione tra i tempi:
$$ (\color{Red}{c\Delta t})^2 = (\color{Green}{c\Delta \tau})^2 + (\color{Blue}{v\Delta t})^2 \\ $$
Che raccogliendo $\Delta t$ ci dà:
$$ \implies \Delta t = \gamma \cdot \Delta \tau \qquad \text{con } \quad \gamma = \frac{1}{\sqrt{1-v^2/c^2}} = \frac{1}{\sqrt{1-\beta^2}} \qquad \text{e } \quad \beta = \frac{v}{c} $$
$\gamma$ viene detto fattore di Lorentz.
Il fattore di Lorentz
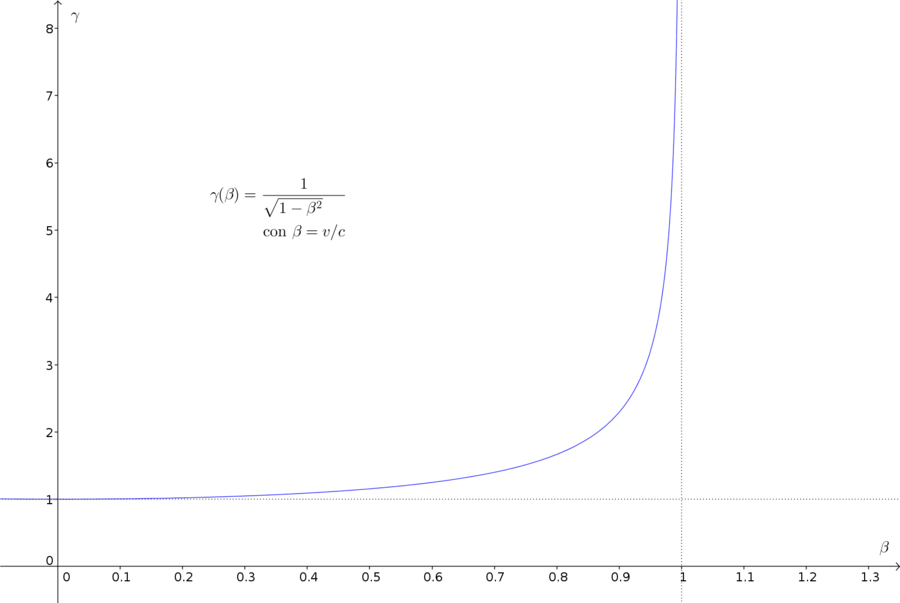
Il fattore $\gamma(v)$, visto come una funzione matematica, ha significato $v<c$, proprio come se $c$ fosse una velocità limite, cosa che è poi confermata dagli esperimenti (si veda al proposito il film del PSSC in fondo a questa pagina). Inoltre è sempre $\gamma > 1$.
A causa del valore molto elevato di $c$ esso è molto prossimo a $1$ per valori ordinari della velocità. In questi casi i tempi misurati sono praticamente identici. In altre parole è necessario utilizzare la relatività solo quando il rapporto $v/c$ è sensibilmente diverso da $0$, ovvero quando la velocità del moto è confrontabile con quella della luce (velocità relativistiche).
Questo grafico mostra che anche per valori di $v < 10 \% c$ il fattore di Lorentz è prossimo a $1$ e si può continuare a usare la fisica classica.
È importante notare che per il principio di Relatività la luce ha la stessa velocità $c$ per entrambi i riferimenti.
Ricapitolando
Abbiamo calcolato il tempo proprio di Albert $\Delta \tau$ attraverso una misura di tempo $c\Delta t$ e una misura di spazio $\Delta x = v \Delta t$.
Avete capito bene. Per conoscere l’intervallo di tempo $\Delta \tau$ trascorso sul treno mi serve sia l’orologio che il regolo, devo cioè unire una misura di tempo con una di spazio. È una premonizione di quanto metterà in luce Minkowski con la sua descrizione dello spazio-tempo a 4 dimensioni.
Ma è l’oggetto della prossima lezione, che servirà a spiegare il paradosso dei gemelli. Il paradosso è il seguente:
- La relatività del tempo è conseguenza del fatto che esiste una velocità limite con cui si propagano i segnali e che questa velocità $c$ è costante in tutti i riferimenti inerziali.
- Ma perché allora quel dannato gemello è tornato più giovane? Dal riferimento dell'astronave è il gemello terrestre ad essersene andato con tutta la Terra appresso, quindi dovrebbe essere costui ad esser rimasto bambino. Che cosa ha rotto questa simmetria?
Film del PSSC: La velocità limite
Questo film mostra una prova sperimentale del fatto che $c$ è la velocità limite.