Quantità di moto

Si può costruire un razzo in cinque minuti. Si prende una bottiglia di plastica, di quelle da un litro e mezzo, abbastanza dura e si pratica un foro nel fondo, di diametro di circa 1 centimetro. Lo si mette su una rampa inclinata come nella figura qui a fianco, oppure infilandolo per il foro appena praticato, non prima di aver inserito qualche goccia (non esagerate se non volete fare un molotov!) facendo entrare l'alcool dalla parte del tappo. Si avvicina la fiamma vicino al foro e questo parte con una bella velocità. L'alcool si incendia e la pressione del vapore fa partire la bottiglia, mentre il gas esce ad alta velocità dal foro.

Si può spiegare quanto visto ricordando il terzo principio della dinamica: le forze tra corpi si presentano sempre a coppie. Quando la bottiglia viene spinta dal gas, essa esercita sul gas una forza uguale e contraria. Il vettore azione $\vec F$ e il vettore reazione $ -\vec F$ hanno quindi stesso modulo e direzione, ma verso opposto. Attenzione però: nessuno dei due corpi è in equilibrio, poichè su ciascuno di essi agisce solo una di queste due forze.

Scriviamo quanto abbiamo detto sopra con la seguente equazione:

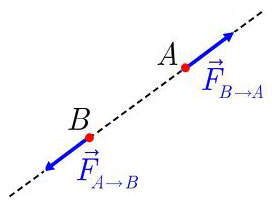
$ \vec F_{B \to A} = - \vec F_{A \to B} $

Ciò può essere letto così: la forza che A applica su B è un vettore uguale e contrario alla forza che B applica su A.

Ricordando che per il secondo principio della dinamica $\vec F = m \vec a$, la stessa equazione può essere riscritta così:

$ m_A \vec a_A = - m_B \vec a_B $

E riscrivendo l'equazione in base alla definizione di accelerazione abbiamo:

$ m_A \large{ \dfrac{\vec v_A - \vec {v_A}_0}{\Delta t} } = -m_B { \dfrac{ \vec v_B - \vec {v_B}_0}{\Delta t} } $

Eliminando la velocità iniziale, che è nulla, e semplificando membro a membro l'intervallo di tempo $ \Delta t $, la precedente equazione diventa particolarmente semplice:

$ m_A \vec v_A = - m_B \vec v_B $

Ciò significa il prodotto tra la massa e il modulo della velocità è costante, quindi la velocità acquistata è inversamente proporzionale alla massa.

Il vettore che si ottiene moltiplicando la massa di un corpo per il vettore velocità si chiama quantità di moto:

$ \vec p = m \vec v $

Pertanto la relazione precedente si può anche esprimere dicendo che la quantità di moto di A è uguale in modulo, ma di verso opposto rispetto a B:

$ \vec p_A = - \vec p_B $

oppure dicendo che la quantità di moto totale, somma delle quantità di moto dei singoli corpi che fanno parte del sistema in studio, è un vettore nullo:

$ \vec p_A + \vec p_B = \vec 0 $

Rispondi a questa domanda: qual era la quantità di moto del sistema razzo + gas prima dell'esplosione? Entrambi erano fermi, quindi zero.

E qual è invece la quantità di moto totale (razzo + gas) dopo l'esplosione? Abbiamo trovato che vale ancora zero. Per questo si dice che la quantità di moto totale del sitema si è conservata, ovvero non è cambiata.

In generale, il principio della conservazione della quantità di moto afferma che:

Ciò si può scrivere anche così:

$$ \vec p_{tot} = \sum_{i=1}^{i=N} \vec p_i = \text{cost} $$

che è un modo abbreviato di scrivere somme molto lunghe:

$$ \vec p_{tot} = \vec p_1 + \vec p_2 + \vec p_3 + \dots + \vec p_n = \text{cost} $$

Se invece il sistema è soggetto a una forza esterna $\vec F_{est}$ allora la quantità di moto totale varia:

$$ \vec F_{est} = \dfrac{ \vec{\Delta p}_{tot} }{\Delta t} $$

Se siete al mare sopra un canotto, non potete metterlo in movimento nonostante tutti gli sforzi che possiate compiere a bordo. Solo una folata di vento (forza esterna) o un colpo di remi può farlo muovere, ma se ci pensate bene remare significa fare forza sull'acqua; la quantità di moto dell'acqua spostata è comunque uguale e contraria a quella del canotto in cui vi trovate, per cui, sebbene la quantità di moto del canotto sia variata, quella del sistema mare + canotto rimane comunque costante.