L'equazione dell'onda armonica
L'animazione che segue mostra la propagazione di un'onda trasversale, come quelle che si possono osservare sull'acqua, per esempio con l'ondoscopio.
Ogni punto dell'onda è un oscillatore armonico, che segue la legge oraria che già conosciamo:
\begin{equation} \label{1} y(t) = Asen(\omega t + \varphi_0) \end{equation}
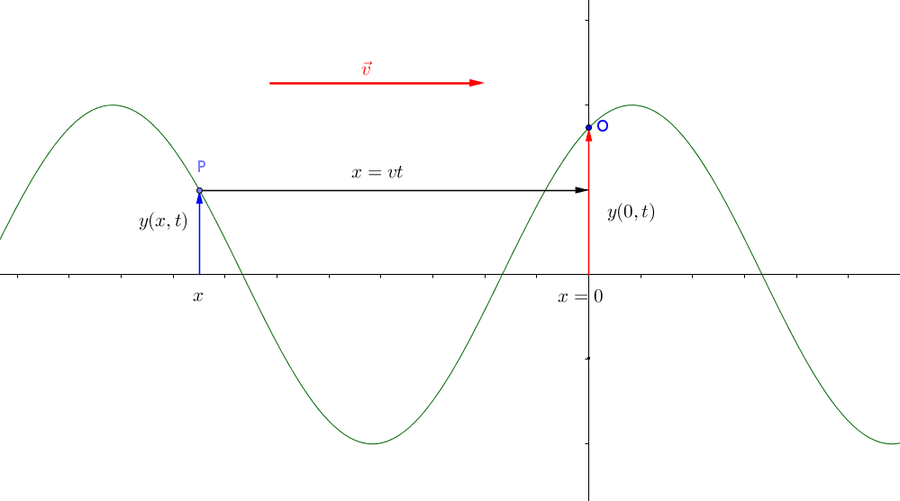
Conoscendo la legge $y(t)$ secondo cui oscilla il punto $O$ nella posizione $x=0$, qual è la legge $y(x,t)$ che rappresenta il moto di un punto materiale $P$ posto in $x$, come nella figura qui sotto?
Se l'onda si muove verso destra esso è in “anticipo di fase” rispetto ad $O$, poichè è stato raggiunto dalla perturbazione un po' di tempo prima. Dobbiamo perciò determinare questo sfasamento per ottenere il suo moto a partire da quello di $O$.
Ma quanto tempo prima di $O$ è stato raggiunto dalla perturbazione? Se la distanza tra $O$ e $P$ è $x$ e l'onda si muove a velocità $v$ abbiamo che
$$ x=vt \Rightarrow t = \frac{x}{v} $$
Se ora l'orologio segna il tempo $t$, il punto $P$ aveva la fase che ora c'è in $O$ al tempo $t - x/v$. Quindi, per trovare la perturbazione in $P$ sostituisco nella ($\ref{1}$)
$$ t \longrightarrow t - \frac{x}{v} $$
Pertanto abbiamo:
$$ y(x,t) = Asen[\omega (t - \frac{x}{v}) + \varphi_0)] $$
E abbiamo quasi finito.
Ricordando che $\omega = 2\pi/T$ e che $v=\lambda/T$ possiamo scrivere la formula precedente in modo più semplice:
$$ y(x,t) = Asen(\omega t - \omega \frac{x}{v} + \varphi_0) = Asen(\omega t - \frac{\color{blue}2\color{blue}\pi}{\color{red}T} \frac{x}{\frac{\color{blue}\lambda}{\color{red}T}} + \varphi_0) $$
Semplificando $\color{red}T$ e introducendo il cosiddetto numero d'onda $k = 2\pi /\lambda$ abbiamo
$$ y(x,t) = Asen(\omega t - kx + \varphi_0) $$
che è la forma finale dell'equazione dell'onda armonica. Essa ci dice come oscilla con il tempo $t$ un punto $x$ qualsiasi dello spazio.
Il segno $-$ davanti a $kx$ indica che il punto $P(x)$ è in anticipo di fase rispetto a $O(0)$ (l'onda ci è passata prima). Se l'onda si muovesse invece vestro sinistra, $P(x)$ sarebbe in ritardo di fase rispetto a $O$ (sarebbe raggiunto dalla perturbazione un po' di tempo dopo) e dovremmo mettere un segno $+$ al posto di quel $-$.