L'effetto Doppler

L'effetto Doppler è il fenomeno secondo cui la frequenza e la lunghezza d'onda, misurate da un osservatore, sono diverse da quelle rilevate in un sistema di riferimento a riposo rispetto alla sorgente dell'onda, come conseguenza del moto relativo tra la sorgente e l'osservatore.

Questo si può vedere nella seguente animazione. L'osservatore che vede arrivare verso di sè la sorgente sperimenta una lunghezza d'onda accorciata rispetto a quella che misura un osservatore che segue la sorgente (il guidatore dell'ambulanza, per intenderci); viceversa, la vede allungata se la sorgente si allontana.

Provate a settare una velocità della sorgente maggiore di $2$ per vedere l'onda emessa da un aereo supersonico, per esempio.

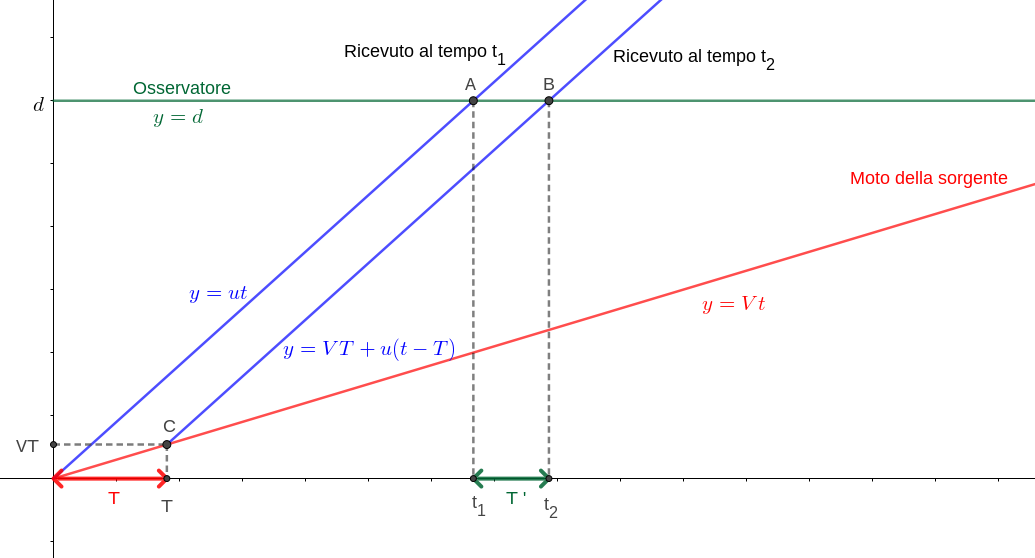
Qui sotto abbiamo un grafico spazio-tempo, dove in verde è rappresentato il moto dell'osservatore, in rosso quello della sorgente e in blu quella dei segnali emessi. I segnali emessi a intervalli di tempo regolari $T$, in questo caso, potrebbero essere i picchi di pressione di un'onda sonora e quindi $f=1/T$ essere la frequenza dell'onda sonora emessa della sorgente. Notare come il periodo $T'$ registrato dall'osservatore può essere rispettivamente minore o maggiore a seconda che sorgente e osservatore siano in avvicinamento o allontanamento.

Ora vogliamo determinare la relazione che vi è tra la frequenza emessa $f$ e la frequenza misurata dall'osservatore $f'$. Per semplificare, supponiamo che l'osservatore sia fermo e la sorgente in movimento. I segnali viaggiano a velocità $u$, mentre la sorgente si muove a velocità $V<u$.

L'intervallo di tempo che separa i due segnali ricevuti dall'osservatore è

$$T'=t_2-t_1$$

Noi dobbiamo calcolare le ascisse $t_1$ e $t_2$ dei punti $A$ e $B$ nel grafico, come intersezione delle rette disegnate.

$$ A \begin{cases} \color{green}{y = d} \\ \color{blue}{y = ut} \end{cases} \qquad \Rightarrow \qquad t_1 = \frac{d}{u} $$

$t_1$ è la soluzione del sistema precedente.

Calcoliamo l'istante di tempo $t_2$ mettendo a sistema le due rette che si incontrano in $B$.

Il punto $C(T, VT)$ in figura rappresenta l'evento in cui la sorgente emette il secondo segnale. Ciò avviene dopo un intervallo di tempo $T$ dall'emissione del primo, quando la sorgente ha percorso uno spazio $VT$, mentre si muove a velocità $V$.

Quindi, ricordando la regola della retta passante per un punto $(x_0,y_0)$ avente coefficiente angolare $m=u$ (la velocità $u$ è il coefficiente angolare nel grafico $s-t$).

$$ y-y_0 = m(x-x_0) $$

Possiamo scrivere la legge orara del secondo segnale come segue:

$$ \color{blue}{y-VT = u(t-T)} $$

Cerchiamo dunque l'ascissa del punto $B$, che altro non è che il tempo $t_2$ in cui il secondo segnale è stato ricevuto dall'osservatore:

$$ B \begin{cases} \color{green}{y = d} \\ \color{blue}{y-VT = u(t-T)} \end{cases} \qquad \Rightarrow \qquad d-VT = u(t-T) \qquad \Rightarrow \qquad ut = d-VT+uT = d + (u-V)T $$

$t_2$ è la soluzione del sistema precedente:

$$ t_2 = \frac{d + (u-V)T}{u} $$

Siamo ora pronti a calcolare il periodo $T'$, così come visto dall'osservatore:

$$ T' = t_2 - t_1 = \frac{d + (u-V)T}{u} - \frac{d}{u} = \frac{u-V}{u}T \\ $$

E' ora importante ottenere la relazione tra le frequenze $f$ ed $f'$, che è il reciproco del precedente:

$$ f' = \frac{u}{u-V}f = \frac{1}{\frac{u-V}{u}}f $$

Ecco la relazione definitiva:

$$ f' = \frac{1}{1-\frac{V}{u}}f $$

Se la sorgente è invece in allontanamento, è sufficiente cambiare di segno la velocità della $V$ della sorgente, quindi la formula precedente diventa:

$$ \begin{equation} \label{1} f' = \left ( \frac{1}{1 \mp \frac{V}{u}} \right ) f \end{equation} $$ dove il segno $-$ vale nel caso di sorgente in avvicinamento, mentre il segno $+$ nel caso di sorgente in allontanamento.

Una volta fatto questo non è difficile ricavare la formula che vale nel caso in cui la sorgente sia ferma e invece l'osservatore sia in movimento:

$$ \begin{equation} \label{2} f' = \left ( 1 \pm \frac{V'}{u} \right ) f \end{equation} $$ Ora il segno $-$ vale se l'osservatore si allontana a velocità $V'$ (frequenza in diminuzione, suono più grave, redshift), mentre il segno $+$ se esso si avvicina (suono più acuto, blueshift).

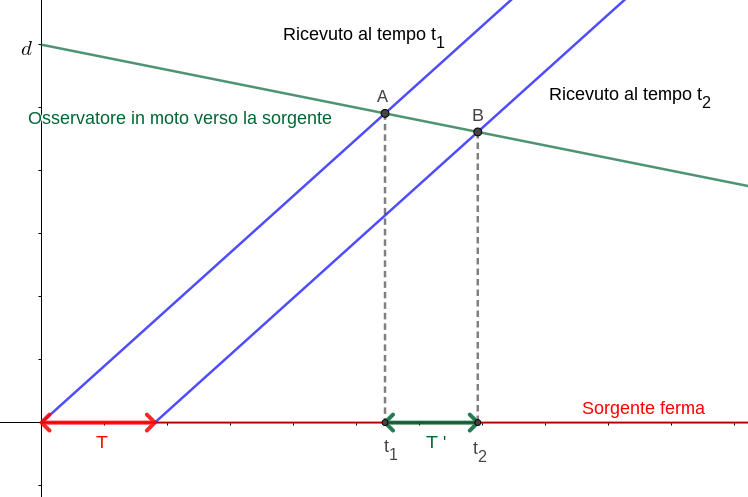
La figura su cui ragionare è questa:

Le formule $\eqref{1}$ e $\eqref{2}$ si possono condensare in un'unica formula dove $V$ e $V'$ sono rispettivamente le velocità della sorgente e dell'osservatore:

$$ \begin{equation} \label{3} f' = \left ( \frac{ 1 \pm \frac{V'}{u} }{1 \mp \frac{V}{u} } \right ) f \end{equation} $$

A partire dall'ultima figura, ricavare la formula $\eqref{2}$.