L'equazione dell'onda armonica

L'animazione che segue mostra la propagazione di un'onda trasversale, come quelle che si possono osservare sull'acqua, per esempio con l'ondoscopio.

Ogni punto dell'onda è un oscillatore armonico, che segue la legge oraria che già conosciamo:

\begin{equation} \label{1} y(t) = Asen(\omega t + \varphi_0) \end{equation}

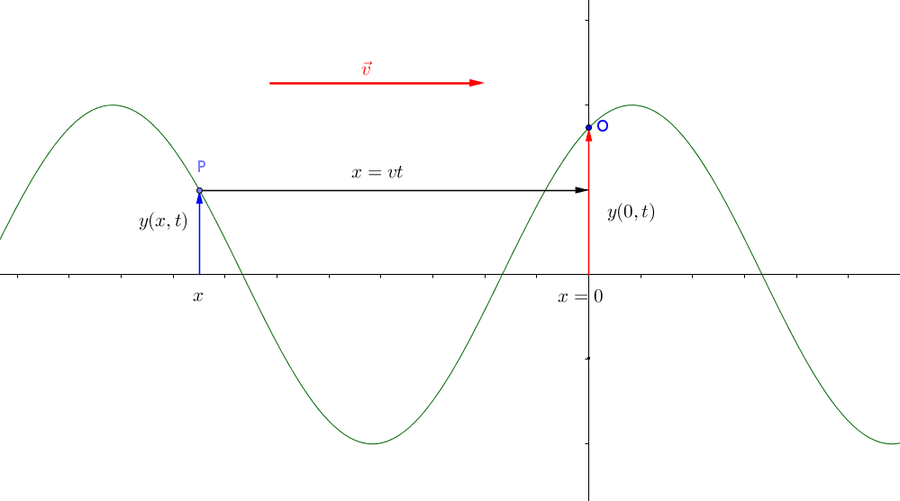
Conoscendo la legge $y(t)$ secondo cui oscilla il punto $O$ nella posizione $x=0$, qual è la legge $y(x,t)$ che rappresenta il moto di un punto materiale $P$ posto in $x$, come nella figura qui sotto?

Se l'onda si muove verso destra esso è in “anticipo di fase” rispetto ad $O$, poichè è stato raggiunto dalla perturbazione un po' di tempo prima. Dobbiamo perciò determinare questo sfasamento per ottenere il suo moto a partire da quello di $O$.

Ma quanto tempo prima di $O$ è stato raggiunto dalla perturbazione? Se la distanza tra $O$ e $P$ è $x$ e l'onda si muove a velocità $v$ abbiamo che

$$ x=vt \Rightarrow t = \frac{x}{v} $$

Se ora l'orologio segna il tempo $t$, il punto $P$ aveva la fase che ora c'è in $O$ al tempo $t - x/v$. Quindi, per trovare la perturbazione in $P$ sostituisco nella ($\ref{1}$)

$$ t \longrightarrow t - \frac{x}{v} $$

Pertanto abbiamo:

$$ y(x,t) = Asen[\omega (t - \frac{x}{v}) + \varphi_0)] $$

E abbiamo quasi finito.

Ricordando che $\omega = 2\pi/T$ e che $v=\lambda/T$ possiamo scrivere la formula precedente in modo più semplice:

$$ y(x,t) = Asen(\omega t - \omega \frac{x}{v} + \varphi_0) = Asen(\omega t - \frac{\color{blue}2\color{blue}\pi}{\color{red}T} \frac{x}{\frac{\color{blue}\lambda}{\color{red}T}} + \varphi_0) $$

Semplificando $\color{red}T$ e introducendo il cosiddetto numero d'onda $k = 2\pi /\lambda$ abbiamo

$$ y(x,t) = Asen(\omega t - kx + \varphi_0) $$

che è la forma finale dell'equazione dell'onda armonica. Essa ci dice come oscilla con il tempo $t$ un punto $x$ qualsiasi dello spazio.

Il segno $-$ davanti a $kx$ indica che il punto $P(x)$ è in anticipo di fase rispetto a $O(0)$ (l'onda ci è passata prima). Se l'onda si muovesse invece vestro destra, $P(x)$ sarebbe in ritardo di fase rispetto a $O$ (sarebbe raggiunto dalla perturbazione un po' di tempo dopo) e dovremmo mettere un segno $+$ al posto di quel $-$.