La circuitazione di un vettore
Per quanto riguarda la definizione di circuitazione di un vettore $\overrightarrow X$ puoi riferirti al tuo libro di testo:
$$ \Gamma (\overrightarrow{X}) = \oint \overrightarrow{X} \cdot \overrightarrow{dl} $$
Soffermiamoci semmai sull'utilità pratica di conoscere il valore della circuitazione. Siamo soliti dire che
Un vettore $\overrightarrow X$ è conservativo se la sua circuitazione è nulla e viceversa
Ma cosa vuol dire questo?
Una risposta non corretta (ho messo il grassetto, eh!! 
Un campo è conservativo se il lavoro fatto su un circuito chiuso è nullo, oppure -il chè è lo stesso- se il lavoro non dipende dal percorso fatto
Il lavoro fatto da chi? Dal vettore $\overrightarrow X$? Questo è vero solo se $\overrightarrow X$ è il vettore forza $\overrightarrow F$; solo allora l'argomento dell'integrale $\overrightarrow F \cdot \overrightarrow{dl}$ corrisponde al lavoro infinitesimo $dL=\overrightarrow{dF}\cdot \overrightarrow{dl}$ fatto lungo il tratto di cammino $\overrightarrow{dl}$. Allora sì che l'integrale di linea $\oint$ indica il lavoro totale lungo tutta la linea chiusa. Ma se $\overrightarrow X$ non è il vettore forza quel prodotto scalare NON rappresenta un lavoro e la definizione precedente è sbagliata.
Se consideriamo il vettore campo elettrico $\overrightarrow E$ l'argomento del prodotto scalare indica la d.d.p. infinitesima $-dV=\overrightarrow{E} \cdot \overrightarrow{dl}$, che è legata al lavoro dalla relazione che conosciamo bene $dL=-dU=-qdV$.
Se consideriamo il vettore campo magnetico la quantità $\overrightarrow B \cdot \overrightarrow{dl}$ non ha nulla a che fare con il lavoro (di quale forza poi?).
Ma allora che informazioni ci dà la circuitazione di un vettore?
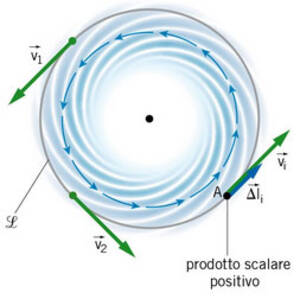
Per capirlo facciamo una similitudine con la dinamica dei fluidi e consideriamo la circuitazione del vettore velocità $\vec v$. Quando le linee di questo vettore sono chiuse il movimento è turbolento e forma dei vortici (come nella figura qui sotto); quando le linee sono aperte il movimento si dice invece laminare.
Se le linee sono chiuse non è difficile capire come la circuitazione possa essere NON nulla nel caso il circuito $\mathcal L$, scelto per fare il calcolo, sia concatenato con il centro del vortice. Infatti il prodotto scalare $\overrightarrow v \cdot \overrightarrow{dl}$ è prevalentemente positivo se il circuito viene percorso nel verso in cui circola il vettore $\vec v$, negativo nel caso contrario; è invece nulla se non si racchiude il centro del vortice.
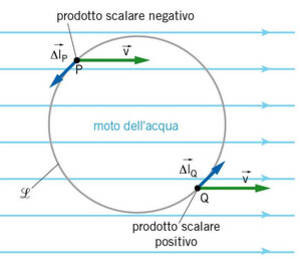
Se invece le linee sono aperte il prodotto scalare tra il vettore $\overrightarrow v$ e l'elemento di circuito $\overrightarrow{dl}$ è in parte positivo e in parte negativo; si può dimostrare (con elementi di matematica più avanzati) che in tal caso è sempre nullo.
Quanto sopra può essere esteso a un campo vettoriale $\overrightarrow X$ qualunque.
La circuitazione di $\vec E$
La terza equazione di Maxwell recita:
$\Gamma (\overrightarrow{E}) = \displaystyle{\oint} \overrightarrow{E} \cdot \overrightarrow{dl}=-\dfrac{d{\phi (\overrightarrow{B})}}{dt}$
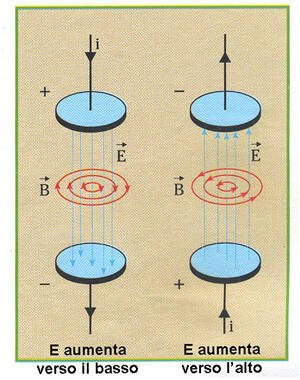
Quindi se il campo elettrico è generato da un campo magnetico variabile, esso NON è conservativo ed ha le linee concatenate con quelle del campo magnetico. Il segno meno suggerisce che le linee del campo elettrico circolano in senso orario se viste dal verso del flusso di $\vec B$ crescente.
Se invece è generato dalle cariche libere (campo elettrostatico) la sua circuitazione è nulla e come sappiamo le linee sono aperte.
La circuitazione di $\vec B$
Questa è la quarta equazione di Maxwell:
$\Gamma (\overrightarrow{B}) = \displaystyle{\oint} \overrightarrow{B} \cdot \overrightarrow{dl}=\mu i + \mu\epsilon\dfrac{d{\phi (\overrightarrow{E})}}{dt}$
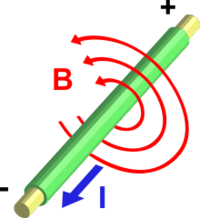
Quindi il campo magnetico è sempre NON conservativo ed ha sempre le linee chiuse. Se è generato da una corrente stazionaria è concatenato con essa (legge di Ampere, primo termine nella equazione precedente)
Lo stesso vale per linee del campo associato ai materiali magnetici, la cui natura è da ricercarsi sempre nella legge di Ampere.
Se invece è generato da un campo elettrico variabile (secondo termine nell'equazione precedente), esso ha le linee chiuse concatenate con il vettore $\vec E$. Queste linee girano in senso antiorario se viste dal verso in cui il flusso di $\vec E$ aumenta.
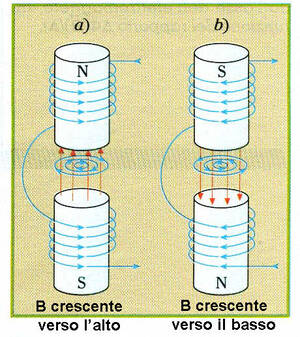
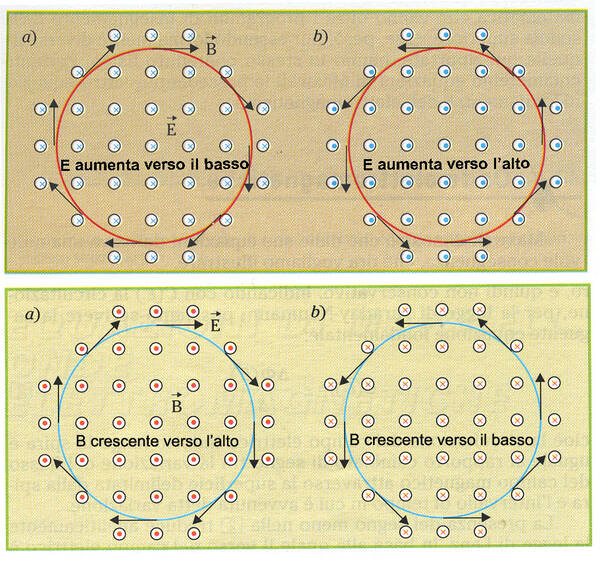
Raffronto tra i due campi indotti
Ecco una figura che raffronta le linee di campo dei campi $\vec E$ e $\vec B$ secondo le ultime due equazioni di Maxwell: