Tutti noi ricordiamo lo stupore provato da piccoli nell'esatto momento in cui abbiamo scoperto l'infinito numerabile (oggi lo chiamiamo Aleph $\aleph_0$). Intorno ai 7 anni d'età decisi di sfidare i numeri e presi a contare fino allo sfinimento, scandendo le enumerazioni con le oscillazioni della mia sedia a dondolo. Nell'arrendermi esausto presi atto dell'infinità dei numeri naturali.

Allora non potevo sospettare che di infinito ne esistesse anche un altro, ancora più grande e “potente”. L'infinito per me era uno solo. La scoperta del suo “fratello maggiore” è infatti possibile solo con le capacità di astrazione che si maturano più avanti nell'età, intorno ai 14 anni, quando si diventa dei piccoli matematici, come siete voi oggi.

Per l'individuazione di questo nuovo infinito ci volle la mente di Georg Cantor (1845 – 1918).

Cantor fu autore di una delle conquiste più incredibili della matematica. Provò che non tutti gli insiemi hanno la potenza del numerabile.

Egli scoprì quello che lui stesso battezzò come $\aleph_1$ (aleph-uno), la potenza del continuo, una nuova e infinitamente più grande cardinalità.

Per definizione, la potenza del continuo è quella dell'insieme dei numeri reali contenuti nell'intervallo $[0; 1[$.

Si dice che un insieme ha la potenza del continuo se i suoi elementi possono essere messi in corrispondenza biunivoca con gli elementi dell'intervallo $[0; 1[$.

Dimostriamo, seguendo proprio il ragionamento di Cantor, che questo insieme non è numerabile (non ha la potenza del numerabile).

Come sappiamo, in questo intervallo ci sono tutti i numeri reali con infinite cifre dopo la virgola (non di periodo 9) del tipo:

$x=0,abcde....$

Il numero di questi elementi è ovviamente infinito, ma la cosa importante è dimostrare che NON si possono enumerare.

Ragionando per assurdo, se $[0; 1[$ fosse numerabile, potrei elencare i suoi elementi mettendoli in successione in questo modo:

${x_1; x_2; x_3; x_4;...}$

In altre parole stiamo immaginando che l'insieme dei numeri reali che vanno da $0$ a $1$ sia così esauribile:

$x_1=0, a_{11} a_{12} a_{13} a_{14} a_{15} ...$

$x_2=0, a_{21} a_{22} a_{23} a_{24} a_{25} ...$

$x_3=0, a_{31} a_{32} a_{33} a_{34} a_{35} ...$

$x_4=0, a_{41} a_{42} a_{43} a_{44} a_{45} ...$

$...$

Ma possiamo sempre trovare un numero reale

$y=0, b_1 b_2 b_3 b_4 b_5 ...$

non compreso in questa serie. Basta infatti scegliere le sue cifre in modo che:

• $b_1 \ne a_{11}$, in questo modo $y$ è diverso da $x_1$ perchè ha almeno la prima cifra diversa da esso;
• $b_2 \ne a_{22}$, in questo modo $y$ è diverso da $x_2$ perchè ha almeno la seconda cifra diversa da esso;
• $b_3 \ne a_{33}$, in questo modo $y$ è diverso da $x_3$ perchè ha almeno la terza cifra diversa da esso;
• $b_4 \ne a_{44}$, in questo modo $y$ è diverso da $x_4$ perchè ha almeno la quarta cifra diversa da esso;
• e così via.

Il numero $y$ è certamente un elemento dell'intervallo $[0; 1[$ diverso da tutti gli altri elementi elencati sopra.

Ne consegue che non possiamo enumerare l'intervallo $[0; 1[$. Perciò dobbiamo ammettere che esiste una cardinalità superiore a quella del numerabile, $%%\%%aleph_1$ per l'appunto.

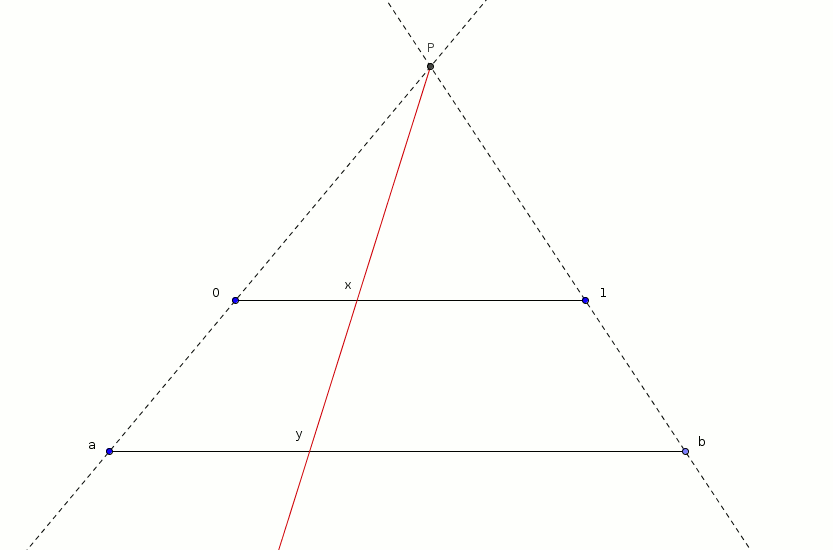
La figura seguente parla chiaro: anche l'intervallo $[a; b[$ ha la potenza del continuo, perchè i suoi punti possono essere messi in corrispondenza biunivoca con i punti dell'intervallo $[0; 1[$.

Insomma, ci sono tanti punti in $[a; b[$ quanti in $[0; 1[$.

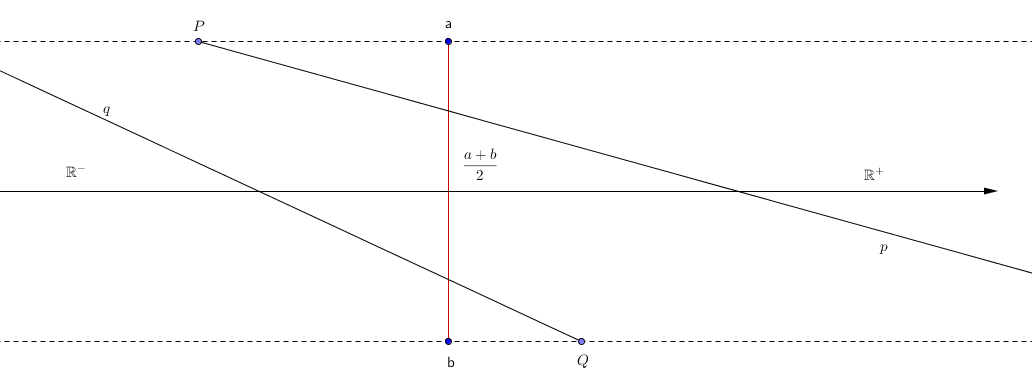
Lo stesso vale per tutta la retta dei reali, come si vede dalla seguente figura:

Se da un punto fisso $P$ si cambia l'inclinazione della retta $p$ si legano con una corrispondenza biunivoca i punti della retta $R^+$ con quelli dell'intervallo $[a; \frac{a+b}{2}[$.

Analogamente se da un punto fisso $Q$ si varia l'inclinaziobne di $q$ si stabilisce una corrispondenza biunivoca tra $R^-$ e l'intervallo $[\frac{a+b}{2}; b[$.

Abbiamo dimostrato che $R$ ha la potenza del continuo.

• Potenza del numerabile
• Bellissimo fumetto sull'argomento
• Ipotesi del continuo