Onde stazionarie

In laboratorio abbiamo prodotto onde stazionarie su una molla e in tubo di Kundt, del quale questa è una immagine dove si vedono chiaramente cinque ventri con i quattro nodi tra di essi:

Possiamo richiamare questi esperimenti con i seguenti filmati:

Un'onda stazionaria è data dalla sovrapposizione dell'onda incidente con quella riflessa.

~ Scarica file ggb ~

Naturalmente la lunghezza d'onda $\lambda$ dei modi di vibrazione (o armoniche) si può determinare con la seguente regola:

\begin{equation} \label{3} \lambda_n = \frac{2L}{n} con\ n \in \mathbb{N} \end{equation}

dove $n$ è la lunghezza della corda, o lo spazio dove è confinata l'onda.

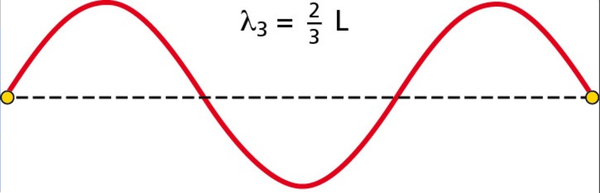
Ad esempio, questa è la terza armonica su una corda:

Questa bella animazione consente di costruire le varie armoniche su una corda in grado di oscillare

~ Scarica file ggb ~

Le oscillazioni in un'onda stazionaria possono determinare un consistente aumento dell'energia dell'onda se sollecitate da una forza esterna che ha la stessa frequenza di vibrazione dell'onda (risonanza). E' il caso del tubo di Kundt visto sopra, ma anche delle oscillazioni che hanno distrutto il Ponte di Tacoma (USA).

Grazie alla prima applet in questa pagina abbiamo intuito che l'onda stazionaria è il risultato della sovrapposizione tra l'onda incidente e l'onda riflessa, che viaggia in senso opposto. Ci proponiamo ora di trovare l'equazione dell'onda risultante, dimostrando che in ogni punto $x$ l'ampiezza non varia con il tempo $t$.

Dobbiamo scrivere le equazioni delle due onde e poi sommarle secondo il principio di sovrapposizione.

L'onda che viaggia verso destra ha fase iniziale $\phi_0 = 0$:

$$ y(x,t) = A \sin(\omega t -kx) $$

L'onda riflessa viaggia verso sinistra, quindi bisogna scambiare $x$ con $-x$. Inoltre, come si vede sempre dalla prima applet in questa pagina, viene riflessa “capovolta” (perchè l'estremo destro non si muove), dunque ha una fase iniziale $\phi_0 = \pi$.

Quindi l'equazione dell'onda riflessa è:

$$ y(x,t) = A \sin(\omega t +kx +\pi) $$

Dal corso di goniometria (archi associati) sappiamo però che

$$ \sin (\alpha +\pi) = -\sin\alpha $$

dunque l'equazione dell'onda riflessa può essere semplificata in questo modo:

$$ y(x,t) = - A \sin(\omega t +kx) $$

Ora le facciamo interferire sommandole, per trovare quella che è l'onda risultante:

$$ y(x,t) = A \sin(\omega t -kx) - A \sin(\omega t +kx) $$

Ci serve la formula di prostaferesi

$$ \sin p - \sin q = 2\sin\frac{p-q}{2} \cos\frac{p+q}{2} $$

Pertanto abbiamo:

$$ y(x,t) = \color{blue} {2A \sin(kx)} \color{red} {\cos(\omega t)} $$

Il termine indicato in blu è l'ampiezza. Si vede che é modulata secondo una funzione $seno$ e non dipende dal tempo. Agli estremi vale $0$ perchè la corda è fissa in quei punti. La parte in rosso rappresenta la legge secondo cui ogni punto $x$ vibra con il tempo $t$.

I nodi sono i punti con ampiezza di vibrazione nulla, quindi:

$$ \sin(kx) = 0 \qquad \Rightarrow \qquad kx = n\pi \qquad \Rightarrow \qquad x = n\frac{\lambda}{2} $$

ovvero vi sono dei nodi ogni mezza lunghezza d'onda.

Siccome l'ampiezza si annulla per $x=0$ e $x=L$ ($L$ lunghezza della corda, o del ponte, o dell'oscillatore considerato) e la funzione $seno$ si annulla per gli archi di $n\pi \ con\ n \in \mathbb{N}$, possiamo scrivere, per $x=L$

$$ \begin{cases} \sin(kL) =0 \implies kL = n\pi \\ k = \dfrac{2\pi}{\lambda} \end{cases} $$

confermando la legge ($\ref{3}$) anche dal punto di vista teorico:

$$ \lambda = \frac{2L}{n} \ con\ n \in \mathbb{N} $$

ovvero la legge che stabilisce i modi di vibrazione di un'onda stazionaria.