Indice
La legge del pendolo
Ecco cosa ci proponiamo di fare
- Imparare a osservare un fenomeno, selezionando le grandezze significative e riconoscendo quali sono invece i fattori di disturbo.
- Fare i conti con gli inevitabili problemi che un esperimento ci mette davanti: le grandezze fisiche e le unità di misura, gli errori nella misura, la loro valutazione.
- Capire qual è la genesi di una legge fisica e al contempo come funziona il metodo scientifico/sperimentale.
Sia chiaro, non è che ci importi particolarmente di quello stupido pendolo. Si tratta solo di un pretesto per studiare e per imparare ciò che ci interessa. Come per l'esperimento riguardante la legge di Coulomb.
Cosa vogliamo misurare
Dopo aver fatto oscillare una massa appesa a un filo ho chiesto quale fosse quella “regolarità” o quella grandezza fisica che caratterizza ciò che si sta osservando.
Uno di voi ha risposto “l'oscillazione”. Ma l'oscillazione non è un qualcosa che possiamo misurare, come può essere la temperatura della stanza, la luminosità del Sole o la lunghezza di un tavolo. Una grandezza fisica è ciò che si può misurare. Di questa oscillazione vogliamo misurare il periodo, ovvero il tempo necessario per fare il percorso di andata e ritorno.
Quali sono le variabili in gioco?
Da cosa dipende questo periodo $T$? Quali sono le grandezze fisiche che influenzano il tempo di oscillazione? Ecco quello che avete detto; qui dapprima abbiamo inserito tutto ciò che può essere importante, consapevoli che alcuni degli iscritti nel registro degli indagati saranno poi licenziati, l'importante è che tra questi ci siano i veri responsabili del fenomeno osservato. Ed erano:
- la gravità
- il volume del grave
- la massa del grave
- il materiale di cui è fatto il grave
- la lunghezza del filo
- l'ampiezza di oscillazione
- e ci aggiungo io che potrebbe essere importante parlare di attrito dell'aria
- altri non me ne ricordo
La gravità, dice subito il buon Giacomo, possiamo subito rilasciarla. Certo che è importante, dice saggiamente, ma in tutte le prove che faremo sarà costante, a meno che non si cambi pianeta. Tutti d'accordo: fuori uno.
Il materiale di cui è fatto il grave in realtà è una ripetizione di massa e volume, ovvero, una volta che studiamo come dipende il periodo dalla massa e poi dal volume abbiamo implicitamente considerato anche la densità del materiale. Fuori due, dunque.
L'ampiezza di oscillazione
Avete visto che ho inaugurato un titolo? Questo vuol dire che è un punto importante! Il problema è: se lascio cadere la massa da un punto molto alto/basso il periodo T è diverso nei due casi? C'è chi dice si, chi no, siamo fifty-fifty insomma.
Davide, però, la sa lunga. Dice: non è una variabile. Infatti, se cade da molto in alto, viaggia più velocemente e ciò può bastare a coprire la maggiore distanza. Dubbi, sberleffi in aula. Qualcuno però incomincia a pensarci seriamente. Chiedo: chi ha ragione? Come si deve fare per sapere se ciò che dice è corretto? Si fa un esperimento e si guardano i risultati. In campo scientifico non ci devono essere autorità, pregiudizi di alcun genere. Cosa è vero e cosa no lo diranno i fatti sperimentali.
Distribuisco tra di voi 5 o 6 cronometri in grado di apprezzare circa mezzo decimo di secondo. Ma è chiaro che il problema non sarà tanto la sensibilità dei cronometri, quanto i nostri tempi di reazione nell'avviare e arrestare il cronometro stesso.
Si fanno due prove da altezze diverse. Avete avuto veramente dei riflessi incredibilmente buoni, perchè generalmente si registrano differenze tra i tempi anche superiori al secondo.
Ecco le misure:
| Partenza in alto | Partenza più in basso |
|---|---|
| 1,3s | 1,5s |
| 1,5s | 1,6s |
| 1,3s | 1,4s |
| 1,5s | 1,4s |
| 1,6s | 1,5s |
| 1,4s | 1,5s |
Se esprimiamo le due misure con il loro errore, calcolato con il criterio del semiscarto massimo, abbiamo:
$$ t_{alto}=(1,4 \pm 0,2)s $$
$$ t_{basso}=(1,5 \pm 0,1)s $$
Ha ragione Davide
La classe si spacca! Ci sono quelli che dicono: «1,4 e 1,5 sono due misure diverse, quindi non possiamo asserire che il tempo di oscillazione sia indipendente dall'ampiezza di oscillazione! Eccheddiavolo!» Ed altri invece: «Nenche per sogno! Non lo vedete che vi sono degli errori sperimentali? Considerando gli errori sperimentali, gli intervalli dei valori possibili nei due casi si sovrappongono!»
Davide ha ragione. O meglio… diciamo che il fisico in questi casi ragiona come lui ha fatto. E cioè dice:
Nei limiti degli errori sperimentali è possibile affermare che il tempo di oscillazione è indipendente dall'ampiezza di oscillazione, sempre che gli errori percentuali commessi siano accettabili.
Ciò non significa che sia necessariamente vero. Solo che il nostro esperimento sembra confermare quell'ipotesi fatta. Per avere una risposta certa e definitiva è però necessario condurre altri esperimenti, ottenere altre prove indipendenti.
Da misure più precise abbiamo notato che, in effetti, l'ampiezza non è rilevante solo nelle piccole oscillazioni. Se essa è molto grande sembra invece influenzare sensibilmente il periodo di oscillazione. Quindi studieremo il fenomeno solo per piccole oscillazioni.
La dipendenza dall'attrito
Abbiamo licenziato questa variabile trovandoci tutti d'accordo che più che altro si tratta di un fattore di disturbo, eliminabile facendo gli esperimenti con delle masse di piombo o comunque di un materiale pesante, il cui moto non fosse disturbato dalla forza di attrito in tempi brevi.
La massa
La cosa si fa seria. Chi l'avrebbe mai detto? Eppure abbiamo visto quello che abbiamo visto! La palla leggera di legno e la sfera pesantissima di piombo oscillano con lo stesso periodo! Però è stato necessario badar bene che nell'esperimento la massa fosse l'unica variabile; quindi la lunghezza del filo, ad esempio, doveva essere perfettamente identica nei due casi.
Il volume
Le due masse di prima non solo avevano massa diversa, ma anche volume diverso! Quindi nemmeno il volume è una variabile che influenza il periodo.
La lunghezza del filo
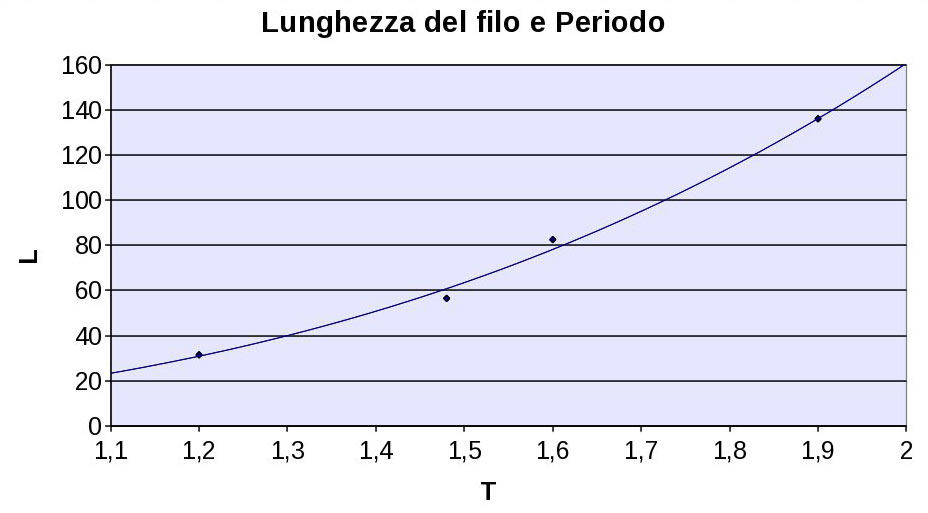
Finalmente abbiamo trovato il responsabile. E' evidente, dagli esperimenti condotti, che il periodo di oscillazione dipende dalla lunghezza del filo. Il periodo aumenta infatti con la lunghezza del filo. Ma di che tipo di dipendenza si tratta? Proporzionalità diretta? Quadratica? E' necessario controllare i rapporti, controllare i grafici, come abbiamo fatto in laboratorio.
Ecco i dati che abbiamo ricavato:
| Periodo e lunghezza del filo | ||||
|---|---|---|---|---|
| Lunghezza del filo $L$ | Periodo $T$ | $L/T$ | $L/T^2$ | $L^2/T$ |
| 136,0 cm | ( 1,9 $\pm$ 0,3)s | 72 | 38 | 9735 |
| 82,5 cm | ( 1,6 $\pm$ 0,2)s | 52 | 32 | 4254 |
| 56,5 cm | (1,48 $\pm$ 0,01)s | 38 | 26 | 2157 |
| 31,5 cm | (1,20 $\pm$ 0,04)s | 26 | 22 | 827 |
Nelle ultime due misure di tempo abbiamo preferito limitare l'errore misurando il tempo di dieci oscillazioni. Gli errori sono stati calcolati con il criterio del semiscarto massimo.
Analisi dei dati
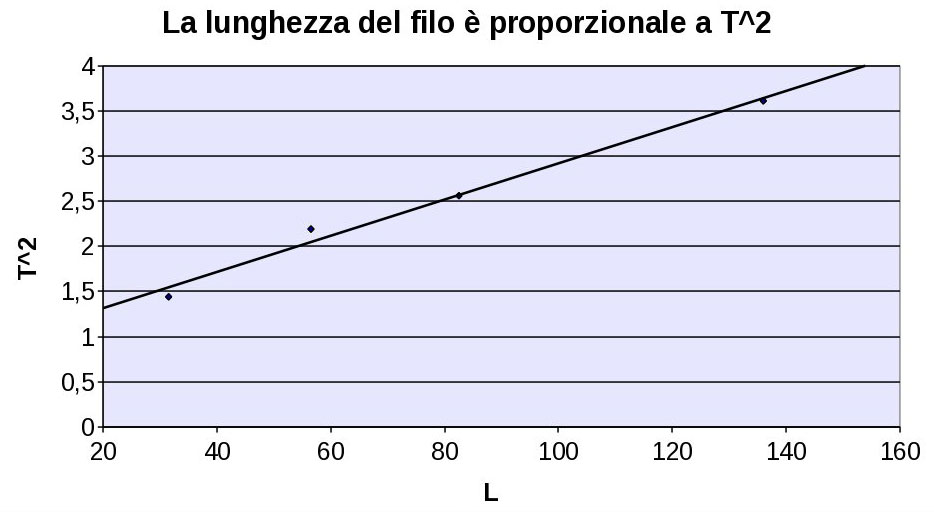
La penultima colonna, quella che calcola il rapporto $L/T^2$, sembra la migliore. I rapporti sono molto più vicini di quanto non succeda nelle altre due colonne. Sembra quindi che vi sia una relazione quadratica, ovvero una proporzionalità diretta tra $L$ e il quadrato di $T$, oppure una proporzionalità diretta tra $T$ e la radice quadrata di $L$.
Vediamo la cosa graficamente. Il grafico $L$ in funzione di $T^2$ (fig. 1) mostra una curva che è stata ricavata disegnandoci sopra proprio un ramo di parabola. Ciò sembra funzionare bene.. naturalmente i punti non sono sopra la curva per via degli errori sperimentali.
Se mettiamo invece negli assi cartesiani $L$ e $T^2$ la tendenza sembra proprio quella di una retta, ovvero una proporzionalità diretta (fig. 2). Infatti i punti che rappresentano i dati sperimentali sembrano disporsi lungo una linea retta.
Per quanto detto possiamo ipotizzare a ragione una legge del tipo:
$$T=k \sqrt{L}$$
Ciò significa che quadruplicando la lunghezza del filo il periodo raddoppia, per esempio.