Il potenziale elettrico
Appunti sparsi e chiarimenti sull'energia del campo elettrico.
Forze conservative
Una forza si dice conservativa se il suo lavoro non dipende dal percorso fatto ma solo dai punti estremi. Poiché invertendo il senso di percorrenza il lavoro cambia di segno, si può anche dire che il lavoro fatto in un cammino chiuso da una forza conservativa è nullo.
Sono conservative tutte le forze centrali, ovvero quelle che orientano il vettore $\vec F$ sempre verso un dato punto, come ad esempio la forza di attrazione gravitazionale tra due masse che si muovono, la forza elettrostatica tra cariche elettriche, o la forza elastica.
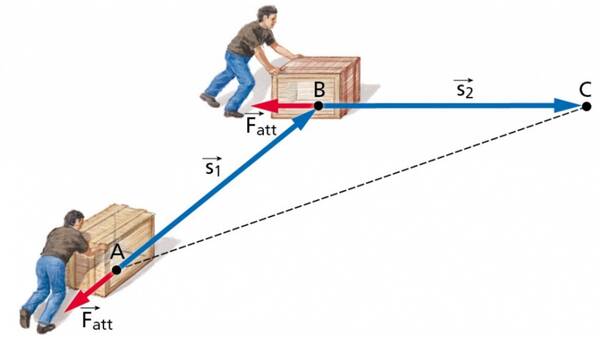
La forza di attrito, invece, non è conservativa, come si intuisce facilmente dalla figura qui sotto. Si vede che non è una forza centrale perchè è sempre contraria allo spostamento. Infatti il lavoro per andare da $A$ a $C$ passando per $B$ è maggiore di quello che si compie lungo il tratto più breve $A \rightarrow C$.
La circuitazione
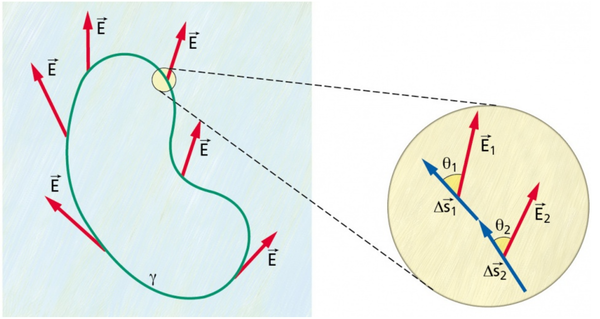
Il calcolo del lavoro della forza elettrica lungo un cammino chiuso è ciò che chiamiamo circuitazione:
$$ W = \Gamma (\vec F) = \sum_{i=1}^n \vec F_i \cdot \vec{\Delta l_i} = 0 $$
Di conseguenza, essendo $\vec E=\dfrac{\vec F}{q}$, ciò equivale a dire che anche la circuitazione di $\vec E$ è nulla:
$$ W = q\Gamma (\vec E) = q\sum_{i=1}^n \vec E_i \cdot \vec{\Delta l_i} = 0 $$
Sappiamo che il calcolo è esatto solo se $ n \to \infty \mbox{ e } \Delta l_i \to 0$. Passando al limite la circuitazione diventa un integrale di linea, che è la maniera più corretta di scriverla:
$$ \Gamma (\vec E) = \oint \vec E \cdot \vec{dl} = 0 $$
che si legge: integrale esteso a un cammino chiuso di E scalare dl. Il circoletto nell’integrale significa proprio che il percorso in cui lo si calcola è chiuso. Notare inoltre che, passando al limite, $ \Delta l $ diventa infinitesimo e si scrive $ dl $. La sommatoria viene sostituita dall’integrale.
Perché sono importanti le forze conservative?
Se il lavoro non dipende dal percorso, possiamo star tranquilli che a prescindere dal cammino seguito l’energia cinetica liberata sarà sempre la stessa. Allora perché non far conto che quell’energia esista in forma latente, o potenziale, ancor prima del moto?
L’energia potenziale
Scegliamo un punto di riferimento a cui attribuiamo per convenzione energia potenziale nulla. Solitamente lo si prende laddove il campo non è più nelle condizioni di compiere lavoro; per il campo elettrico si sceglie un punto all’infinito (lo stesso per il campo gravitazionale). L’energia potenziale in un punto è il lavoro che il campo elettrico compie per portare la carica di prova da quel punto all’infinito, ovvero fuori dall’azione dello stesso campo elettrico.
Energia potenziale del campo generato da una carica positiva
Facciamo l’esempio di una carica puntiforme positiva, nel quale campo abbiamo la nostra carica di prova, per convenzione positiva.

Chiedetevi se il lavoro fatto dal campo per portare la carica all’infinito è positivo o negativo. Fatto? Le due cariche si respingono per loro stessa natura, vero? Il campo applica una forza che ha lo stesso verso dello spostamento e il lavoro (definito come il prodotto scalare di $\vec F$ e $\vec s$) è positivo. Infatti la forza è motrice, non frenante.
Di conseguenza l’energia potenziale della carica di prova $+q$ è positiva, ed è numericamente uguale al numero di joule di lavoro fatto. L’energia potenziale a distanza $r$ è data da:
$$ U(r) = \frac{1}{4\pi \epsilon}\frac{Qq}{r} $$
Banalizzando si vede che è positiva perché entrambe le cariche hanno segno positivo ($+\times +=+$)
Energia potenziale del campo generato da una carica negativa
Bene, ora è una carica negativa a creare il campo elettrico, che viene avvertito da una carica di prova, per convenzione sempre positiva.

Domanda: se la carica di prova viene spostata all’infinito, il campo elettrico fa un lavoro positivo (a favore del moto) o negativo (si oppone al moto)? Ora le due cariche si attraggono, e manco per sogno che la carica di prova si muove per uscire dal campo a distanza infinita. Ci vuole una forza esterna per fare questo. Immaginate che sia la vostra mano a fare questo lavoro, tirando la carica di prova contro le forze attrattive del campo elettrico, che è frenante rispetto a questo moto contro natura. Allora? Avete capito che segno ha il lavoro del campo? Abbiamo detto che si oppone al moto (prodotto scalare minore di $0$), dunque è negativo. Dunque anche l’energia potenziale è negativa, poiché l’abbiamo definita come il lavoro che fa il campo quando si porta la carica di prova all’infinito.
$$ U(r) = \frac{1}{4\pi \epsilon}\frac{-Qq}{r} $$
Si vede che è negativa, no? ($+\times -=-$).
Ricorda: quando vi è uno stato legato causato da un’attrazione tra corpi l’energia è negativa.
Passiamo ora al caso generale
Nel primo caso considerato sopra, quello repulsivo, man mano che le forze del campo agiscono, l’energia potenziale diminuisce come $1/r$. Il lavoro fatto dal campo equivale a questa diminuzione:
$$ W=-\Delta U $$
Insomma, il lavoro del campo è uguale alla diminuzione dell’energia potenziale.
Come dite? Lo so, lo so… ho capito! L’Amaldi scrive $+$… lasciatelo perdere, è una questione di convenzioni, abbiamo ragione entrambi. Per colpa sua mi tocca scrivere questi appunti, quindi silenzio oppure beccatevi l’Amaldi!
Anche nel caso attrattivo vale la relazione precedente. Quando noi allontaniamo le cariche il valore della distanza aumenta e $U$ tende a $0$ passando per valori negativi. Quindi l’energia potenziale aumenta, assumendo valori sempre meno negativi fino a $0$ quando arriva all’infinito; per contro il lavoro del campo è negativo.
Certo, sarebbe più naturale scrivere la relazione precedente così, ma è lo stesso:
$$ -W=\Delta U $$
questo perché l’aumento dell’energia potenziale è uguale al lavoro negativo fatto dal campo.
Beh, se non l’avete capito adesso buttatevi dalla finestra e calcolate come la vostra energia potenziale diminuisca convertendosi in energia cinetica a causa del lavoro fatto dalla gravità. Durante la caduta capirete tutto e vi pentirete del gesto infausto appena compiuto. Per fortuna c’è un materasso, sicché tornerete su facendo aumentare $U$ mentre la gravità fa lavoro negativo. Mentre rimbalzate più volte cercate di considerare le cose in termini di potenziale, anziché di energia potenziale.
Il potenziale
L’energia potenziale è una proprietà della carica di prova. Osservate dalla formula che dipende dal suo valore:
$$ U(r) = \frac{1}{4\pi \epsilon}\frac{Qq}{r} $$
Il potenziale invece è una proprietà dei punti dello spazio. Nei punti di una regione di spazio che è sede di un campo elettrico c’è un valore del potenziale elettrico a prescindere dal fatto che vi poniamo o meno una carica di prova per valutare l’energia in quel punto.
Viene definito così:
$$ V = \frac{U}{q} $$
Perciò si misura in $ Joule/Coulomb $, ovvero in $Volt$. Nel caso del campo generato da una carica puntiforme:
$$ V(r) = \frac{1}{4\pi\epsilon}\frac{Q}{r} $$
Si vede o non si vede che è indipendente dalla carica di prova? Dipende solo da ciò che ha generato il campo, cioè $Q$.
La relazione tra energia potenziale e lavoro può essere ora scritta così:
$$ W=-\Delta U = -q\Delta V $$
Il potenziale in un punto, analogamente all’energia potenziale, è il lavoro fatto dal campo elettrico quando le cariche vengono allontanate all’infinito fratto la carica di prova.
La barriera di potenziale
La carica $Q$ crea il campo, e tutt’intorno vi è un potenziale positivo. In ogni direzione esso decresce come un ramo d’iperbole, ovvero come la funzione $1/r$.

Quando una carica di prova passa da $A$ a $B$, il campo fa un lavoro positivo, facendo diminuire sia il potenziale che l’energia potenziale.
Guardando la figura viene voglia di dire che il potenziale è “caduto”, e infatti è una dicitura accettata. Sotto un certo punto di vista la carica $q$ che viene respinta precipita giù dalla barriera di potenziale.
Ora, cerchiamo di capire che succede se la carica di prova viene sparata ad alta velocità contro la barriera. Se l’urto non è frontale viene deviata di lato. Se invece lo è, la sua energia cinetica cosa fa? Diminuisce! E dove va a finire? Viene usata per far lavoro contro le forze del campo, ovvero per scalare la barriera, finché ce la fa ovviamente. Poiché l’altezza è infinita non ce la farà mai a toccare la carica $Q$; prima o poi esaurirà l’energia cinetica e invertirà il moto “precipitando”.
Questo esempio ci fa notare come il moto naturale (spontaneo) sia quello che fa diminuire l'energia potenziale. Per aumentare l'energia potenziale bisogna fornire energia dall’esterno.
Per quanto riguarda invece il potenziale, le cariche positive si muovono spontaneamente verso il potenziale più basso. Che vorrebbero invece fare le cariche negative per loro natura? Piacerebbe loro muoversi verso potenziali più bassi o più alti? Prova tu a rispondere.
La buca di potenziale
Questo è il caso del campo generato da una carica negativa. Il potenziale è sempre sotto lo zero, e si annulla solo all’infinito. Anche qui il moto spontaneo delle cariche positive è quello che fa diminuire il potenziale e l'energia potenziale (vale lo stesso per le cariche negative?).
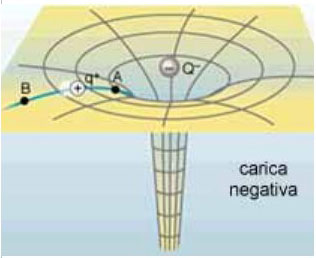
Se vogliamo cavare la carica di prova dalla buca dobbiamo lavorare contro il campo, un po’ come se dovessimo estrarre l’acqua da una miniera. Viceversa la carica $q$ è destinata a precipitare nella buca, a meno che non abbia energia cinetica sufficiente per orbitare a una certa distanza da $-Q$, come una biglia nella roulette.
In un atomo di idrogeno le cose non sono molto diverse; si invertono solo i segni delle due cariche, ma il discorso è identico.
L’elettrone, prigioniero dell’atomo, non ha energia cinetica sufficiente ad azzerare l’energia totale. L’energia di legame è proprio il lavoro che occorre fare dall’esterno per ionizzare l’atomo portando l’elettrone fuori dal campo elettrico del protone.
Buonanotte